Одним росчерком [Яков Исидорович Перельман] (fb2) читать постранично
[Настройки текста] [Cбросить фильтры]
- 1
- 2

ОДНИМ РОСЧЕРКОМ
Вычерчивание фигур одной непрерывной линией
Задача о Кенигсбергских мостах
Внимание гениального математика Эйлера привлекла однажды: своеобразная задача, которую он высказал в такой форме:«В Кенигсберге есть остров, называемый Кнейпгоф. Река, омывающая его, делится на два рукава (см. рис.), через которые перекинуто семь мостов: а, b, с, d, e, f, g

„Можно ли обойти все эти мосты не побывав ни на одном из них более раза?“ „Некоторое утверждают, что это возможно. Другие, напротив, находят такое требование неосуществимым“».Каково же ваше мнение, читатель?
Что такое топология?
Задаче о Кенигсбергских мостах Эйлер посвятил целое математическое исследование, которое было в 1736 г. представлено в Петербургскую Академию наук. Работа эта начинается следующими строками, определяющими, к какой области математики относятся подобные вопросы:«Кроме той отрасли геометрии, которая рассматривает величины и способы измерения и которая тщательно разрабатывалась еще в древности, Лейбниц первый упомянул в другой отрасли, названной им „геометрией положения“. Эта отрасль Геометрии занимается только порядком расположения частей фигуры друг относительно друга, отвлекаясь от их размеров». *)
«Недавно мне пришлось слышать об одной задаче, относящейся к геометрии положения, и я решил изложить здесь, в виде примера найденный мною способ решения этой задачи».Эйлер имеет в виду задачу о Кенигсбергских мостах. Рассуждений великого математика мы здесь излагать не станем, а ограничимся сейчас краткими соображениями, подтверждающими его окончательный вывод. Он состоит в том, что требуемый задачей обход невыполним.

Разбор задачи
Для наглядности заменим рисунок расположения речных рукавов упрощенной схемой (см. рис.). В предложенной задаче размер острова и длина мостов никакого значения не имеет (такова, мы знаем, характерная особенность всех топологических задач: они не зависят от относительных размеров частей фигуры).
Поэтому мы можем местности А,В,C,D (рис. 1) заменить на схеме точками соответствующего наименования, в которых встречаются пути обхода. Задача сводится теперь, как видим, к тому, чтобы начертить фигуру 2 одним, росчерком, не отрывая пера от бумаги и не проводя ни одной линии дважды. Покажем, что фигуру нашу начертить одним росчерком нельзя. В самом деле, в каждую из узловых точек A, B, C, D, надо притти по одному из путей и затем эту точку покинуть по другому пути, исключение составляет только начальная и конечная точки: в первую не надо ниоткуда приходить, вторую нет надобности покидать. Значит, для возможности непрерывного обхода нашей фигуры необходимо, чтобы во всех узловых точках, кроме двух, сходилось либо по 2, либо по 4 пути, — вообще четное число путей. В нашей же фигуре в каждой из точек А, В, С, D сходится как раз нечетное число линий. Поэтому начертить ее одним росчерком нельзя; невозможно, следовательно, и обойти Кенигсбергские мосты требуемым образом.
Семь задач
Попытайтесь нарисовать одним росчерком каждую из следующих семи фигур. Помните требования: начертить все линии заданной фигуры, не отрывая пера от бумаги, не делая никаких лишних штрихов и не проводя дважды ни одной линии.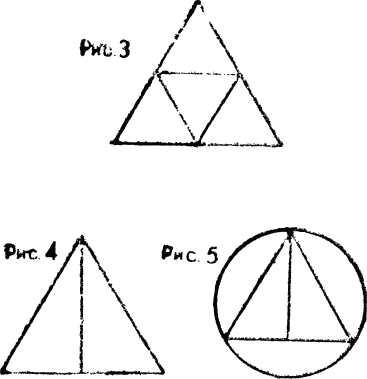

Немного теории
Попытки вычерчивания непрерывной линией фигур 3–9 приводят к неодинаковым результатам. Некоторые фигуры удается вычерчивать, с какой бы точки ни начинать вести первую линию. Другие вычерчиваются одним росчерком в тех лишь случаях, когда начинают с определенных точек. Наконец, третьи вовсе не поддаются вычерчиванию одной непрерывной линией. Чем обусловлено подобное различие? Существуют ли признаки, позволяющие установить заранее, поддается ли данная фигура вырисовыванию одним росчерком и, если поддается, то с какой точки следует начинать черчение? Теория дает на эти вопросы исчерпывающие ответы, и мы сейчас познакомимся с некоторыми положениями этой теории. Условимся называть «четными» те точки фигуры, в которых сходится четное число линий, — в отличие от точек «нечетных», в которых встречается нечетное число линий. Можно доказать (приводить доказательств не станем), что какова бы ни была фигура, нечетных точек в ней либо нет совсем, либо их имеется 2, 4, 6 — вообще четное число. Если нечетных точек в фигуре нет, то она- 1
- 2

Последние комментарии
14 часов 4 минут назад
1 день 24 минут назад
1 день 12 часов назад
1 день 20 часов назад
1 день 21 часов назад
1 день 22 часов назад