Новый взгляд на мир [Фрактальная геометрия] (Мир математики. т.10.) [Мария Изабель Бинимелис Басса] (fb2) читать онлайн

Мария Изабель Бинимелис Басса «Мир математики» № 10 «Новый взгляд на мир. Фрактальная геометрия»

Моему доверенному лицу в мире фракталов Антони Бенсени и в память о Хуане Фемениасе

Предисловие

40 лет назад никто не слышал о фракталах. Ученые имели определенное представление о них, но даже самого понятия «фрактал» тогда еще не существовало. В своей книге «Новый ум короля» профессор Роджер Пенроуз придерживается мнения, что математика — это череда открытий уже существующего, а не изобретений нового. Математические объекты — это некие идеальные представления, которые отражают кажущийся порядок в определенных аспектах окружающего нас мира.

Облака, деревья, молнии, сталактиты и даже павлиний хвост — все эти объекты можно описать с помощью фрактальной геометрии подобно тому, как Землю можно представить в форме шара, а моллюсков-наутилусов — в виде спирали. Земля не является идеальной сферой или идеальным эллипсоидом. Однако подобная модель очень полезна, например, при вычислении времени и места затмений, и обеспечивает достаточную точность.

Перелом в описании Вселенной произошел, когда ученые обратили внимание на новые геометрические объекты, ранее считавшиеся случайными или не имеющими особого значения. Эти новые объекты имели неравномерную, а порой и хаотичную структуру. В попытках структурировать этот «беспорядок» были найдены правила, которые до этого игнорировались, шаблоны, которые повторялись при разном масштабе наблюдений. Именно тогда, как объясняет Нассим Николас Талеб в своей книге «Черный лебедь», все элементы головоломки, известные еще Платону, Ципфу и Юлу, сошлись в руках Бенуа Мандельброта. Согласно Талебу, именно Мандельброт связал случайность (на поверку оказавшуюся мнимой) и геометрию и тем самым привел вопрос к логическому завершению. Чтобы подтвердить свою теорию, ему пришлось обратиться к работам никому не известных на тот момент математиков.

Спустя некоторое время обнаружились множественные взаимосвязи между этим новым разделом математики и другими науками: биологией, геологией, урбанистикой, технологией и даже искусством. Почти одновременно с этим на свет появилось гак называемое множество Мандельброта, где в результате простого последовательного возведения числа в квадрат появляется удивительное по красоте и сложности изображение. Оно не только является порождением нашего разума, но и содержит в себе особый мир.

Математические обозначения находятся вне времени: они описывают реальность, в которой мы живем, и одновременно выходят далеко за рамки материального мира. С момента зарождения цивилизации человек стремился познать законы Вселенной. Фракталы — это новый взгляд на мир, который мы только-только начали постигать.

Глава 1 Развитие геометрии: Мандельброт против Евклида

С давних пор люди пытались понять строение космоса. Они стремились найти законы Вселенной, которым подчиняется движение планет и форма галактик, искали формулы, позволяющие предсказать падение предметов, старались понять полет птиц, изучали анатомию живых существ и строение человеческого разума.

В целом космос делится на две части: микрокосмос и макрокосмос. Макрокосмосом называют множество объектов Вселенной, которые по размерам сопоставимы с нашей планетой, Солнечной системой, галактикой или созвездиями. Микрокосмос, напротив, образуют все объекты, которые по размерам сопоставимы с человеком или даже меньше его. Например, сюда относятся органы нашего тела, вирусы и молекулы. Человеку всегда было интересно то, что нельзя увидеть или предсказать, и это любопытство двигало его в дали макрокосмоса и в глубины микрокосмоса.

Еще с древних времен считалось, что между микрокосмосом и макрокосмосом есть взаимосвязь. В Древней Греции верили, что элементы всего сущего, начиная от макрокосмоса и заканчивая микрокосмосом, воспроизводятся по одним и тем же схемам и правилам. Древнегреческие философы, увидев, что соотношение 1,6180…, позднее названное золотым сечением, присутствует во всех явлениях природы, попытались дать этому рациональное объяснение и тем самым совершили первый шаг к унификации микро- и макрокосмоса. В арабских источниках 650 г. встречаются переведенные тексты изумрудной скрижали, которую, по легенде, написал Гермес Трисмегист (от его имени происходит слово «герметичный»). В изумрудной скрижали раскрываются тайны «первичнои материи» и ее видоизменении, описывается «великое делание» — основной рецепт алхимии. Вторая заповедь скрижали гласит: «То, что находится внизу, соответствует тому, что пребывает вверху; и то, что пребывает вверху, соответствует тому, что находится внизу, чтобы осуществить чудеса единой вещи». Основная цель алхимии — понять таинственную связь между микрокосмосом и макрокосмосом и тем самым обрести мудрость.

Желание греков унифицировать микро- и макромиры нашло отражение в недавно появившемся разделе математики. В одной из многочисленных областей геометрии рассматриваются два основных понятия: самоподобие и непрерывность. Оба эти понятия со временем постепенно уточнялись и дополнялись. Именно о них мы подробно поговорим далее и расскажем о некоторых весьма интересных математических конструкциях.

МАКРОКОСМОС И МИКРОКОСМОС

Американский архитектор финского происхождения Ээро Сааринен говорил о необходимости создания многомерной модели реальности. По его словам, при проектировании всегда следует начинать с больших и меньших объектов, что поможет в конце концов найти оптимальный вариант. Сааринен вдохновил американского архитектора и дизайнера Чарлза Имза на создание научно-популярного короткометражного фильма «Десятые степени» (1968). Имз снял его совместно со своей супругой Рэй Имз на основе книги Киза Боеке «Космический взгляд» (1957). Книга состояла из последовательности изображений разного размера, начиная от масштабов нашей галактики и до картин «человеческого масштаба». На ее страницах можно увидеть человека в городском парке и еще меньшие изображения, показывающие микрокосмос живых существ и строение материи. Центральные части всех снимков и рисунков совпадают; тем самым образуется взаимосвязь между галактиками и атомами, макрокосмосом и микрокосмосом. Это помогает понять соотношение масштабов в теории и на практике. Увидеть все это «вживую» можно на сайте www.powersof10.com.

* * *

В основе практически всей современной науки лежит математика, поэтому не зря степень развития науки или цивилизации оценивают по тому, насколько она «математична». Основным инструментом научного и технического прогресса во всех цивилизациях была геометрия, и в то же время она развивалась благодаря растущим потребностям науки и техники.

Наглядный пример подобного симбиоза являет собой китайская цивилизация. Китайцы бесстрашно пересекали океаны, не боясь затеряться в открытом море, так как имели в своем распоряжении очень точные карты. Геометрию также использовали египтяне при постройке пирамид. В свою очередь, математик и астроном Аристарх Самосский (310–230 гг. до н. э.) с высокой точностью рассчитал расстояние от Земли до Луны. Еще один математик и астроном, Эратосфен (276–194 гг. до н. э.) родом из Кирены, располагая крайне примитивными средствами измерений, тем не менее очень точно вычислил диаметр Земли. Значительно позднее благодаря телескопам-рефлекторам были открыты миллионы звезд, а при помощи параллакса стало возможным найти расстояние до некоторых ближайших звезд.

Согласно историку и географу Геродоту Галикарнасскому, в Древнем Египте была очень развита геометрия и греки считали именно египтян своими учителями и создателями геометрии. Хотя сохранилось лишь несколько чисто практических формул для вычисления длин, площадей и объемов, нам известно, что с их помощью египтяне вычисляли размеры земельных участков, чтобы восстанавливать их после ежегодных разливов Нила. Отсюда происходит слово γεωμετρια — геометрия, измерение Земли» (от древнегреческого γη — Земля и μετρε'ω — измеряю). Слово «геометрия» уже было известно во времена Эратосфена, и когда он поистине гениальным способом вычислил диаметр Земли, то придал словам «измерение Земли» новый смысл.

Геометрия изучает свойства пространства и способы измерения длин, углов и поверхностей различных объектов, которые встречаются в повседневной жизни. Она тесно связана с тем, как мы познаем реальность. Вся информация, которую мы получаем из окружающего мира, все, что мы видим, слышим и ощущаем, выражается в первую очередь в терминах геометрии, и это влияет на все, что мы делаем. Комнаты в домах и земельные участки издавна имеют прямоугольную форму. Траектория падения предметов, орбиты вращения планет, форма моллюсков-наутилусов, форма, которую принимает провисший электрический провод, — все это примеры фигур, изучаемых в классической геометрии. Другие фигуры были неизвестны науке вплоть до начала XIX века.

ЭРАТОСФЕН И ВЫЧИСЛЕНИЕ РАДИУСА ЗЕМЛИ

Люди поняли, что Земля имеет форму шара, очень давно. На это указывали следующие факты: на севере и на юге видимое положение звезд на небе заметно отличалось; когда корабли пропадали из виду на горизонте, последними виднелись мачты; тень Земли на Луне во время затмений имела круглую форму и так далее. Эратосфен, который возглавлял Александрийскую библиотеку (за несколько лет до него эту должность занимал сам Евклид), изобрел очень простой метод для вычисления земного радиуса.

Из папирусов его библиотеки нам известно, что в Сиене (в настоящее время — Асуан) в день летнего солнцестояния предметы не отбрасывали тени и свет проникал на дно колодцев. Предположив, что Александрия находится точно на север от Сиены (в действительности Александрия расположена немного северо-восточнее) и Солнце настолько далеко от Земли, что его лучи параллельны друг другу, Эратосфен измерил длину теней в Александрии в день летнего солнцестояния. Так он показал, что Сиена отстоит от Александрии на 7°12′. Позднее он уточнил расстояние, которое проходили между этими городами караваны торговцев. Оно оказалось равным 5 000 стадиев (хотя точная цифра содержалась и в книгах Александрийской библиотеки). На основе этих данных он произвел нужные вычисления с помощью тригонометрических методов. Приняв один стадий Эратосфена за 185 м, получим вычисленное им значение радиуса Земли в 6 616 км (ошибка составила примерно 17 %). Однако некоторые исследователи считают, что Эратосфен использовал в расчетах египетские стадии — 300 локтей по 52,4 см каждый. В этом случае найденная им длина окружности, проходящей через полюса, равняется 39 614,4 км, что отличается от современного значения в 40 008 км менее чем на 1 %.

* * *

Если судить по тому, о чем мы только что рассказали, может показаться, что геометрия носит чисто практический характер, но история показывает, что это не совсем так. Иногда предметом изучения геометрии становились объекты, невидимые глазу. В трактате «Тимей» Платон говорит о поисках некоего вещества, из которого должно состоять все сущее. Он перечисляет пять основных элементов: огонь, воздух, земля, вода и эфир. Путем логических рассуждений в соответствие каждому элементу ставится геометрическая фигура: огню — тетраэдр, воздуху — октаэдр, земле — гексаэдр, то есть куб, воде — икосаэдр, эфиру — додекаэдр. Эти пять многогранников, которые позднее стали называть Платоновыми телами, — единственные существующие правильные многогранники. (Вспомним, что многогранник называется правильным, если его грани являются правильными многоугольниками, равными между собой, и в каждой вершине сходится одинаковое число граней.)

Изображения Платоновых тел, созданные Леонардо да Винчи для знаменитого шедевра Луки Пачоли «О божественной пропорции» (Венеция, 1509).

В свою очередь, немецкий астроном Иоганн Кеплер (1571–1630) в течение двадцати лет безуспешно пытался описать Солнечную систему как гармоничную совокупность сфер и правильных многогранников. Он предположил, что орбиты шести известных в то время планет лежат на поверхностях шести сфер, разделенных вписанными в них многогранниками.

Наибольшая сфера заключает в себе орбиту Сатурна и отделена от орбиты Юпитера кубом. Между Юпитером и Марсом Кеплер поместил тетраэдр, между Марсом и Землей — додекаэдр, между Землей и Венерой — икосаэдр, между Венерой и Меркурием — октаэдр. Вся эта конструкция соответствовала результатам наблюдений, за исключением орбиты Меркурия.

Вверху — гравюра авторства Фредерика Маккензи, на которой изображен Иоганн Кеплер. На иллюстрации внизу изображена модель Солнечной системы из пяти Платоновых тел, которую описал Кеплер в своей книге Mysterium Cosmographicum («Тайна мира», 1596).

Кеплер не смог объяснить разницу в восемь минут дуги между рассчитанной им круглой орбитой («совершеннейшей из траекторий») и результатами наблюдений астронома Тихо Браге (1546–1601). Разочарованный Кеплер понял, что от применения окружностей нужно отказаться. В конце концов он выстроил свою модель на основе эллипсов — в то время эта фигура использовалась редко. Сведения об эллипсах были известны благодаря книге Аполлония Пергского, которая уцелела при разрушении Александрийской библиотеки. Кеплер обнаружил, что эллиптическая орбита идеально соответствует результатам наблюдений Браге.

Ужасное божество

Оставим ненадолго хитросплетения геометрии и рассмотрим подробнее, почему люди так настойчиво стремились понять устройство окружающего мира. Для этого будет полезно ввести новое понятие — хаос.

Космос и хаос — две противоположности. Космос часто считают синонимом упорядоченности, а хаос — то же самое, что и беспорядок. Как и во многих других мифологиях о происхождении богов, в «Теогонии» греческого поэта Гесиода воплощением хаоса была богиня Хаос^[1]. С космосом, напротив, не связывалось какое-либо божество. Слово «хаос» происходит от протоиндоевропейского корня ghen, означающего «пустой» или «раскрывшийся». Возможно, в те времена, когда было придумано слово «хаос», оно означало пространство, заключенное между небом и землей. Позднее в силу различных причин этим словом стали обозначать беспорядок.

С самых истоков цивилизации люди наблюдали необъяснимые явления, которые удивляли и внушали страх. О подобных явлениях часто говорят, что они принадлежат к миру хаоса. Согласно «Теогонии» Гесиода, написанной примерно 2700 лет назад, боги появились, чтобы образовать порядок из хаоса и тем самым защитить людей. История науки следует по тому же пути: ученые стремятся найти порядок среди хаоса, и в этом им неизменно помогает математика.

Люди, подобно богам, пытались упорядочить хаос. Платон в свое время утверждал, что природа строится по математическим законам, и на протяжении веков многие ученые разделяли его точку зрения. Для проявлений упорядоченности в природе необходимо найти математическое объяснение. Но как быть с теми явлениями, которые не вписываются в общий порядок?

По мнению популяризаторов науки Иена Стюарта и Мартина Голубицкого, в хаосе среди кажущегося беспорядка формируются новые формы упорядоченности. Но вне зависимости от того, какое определение мы дадим хаосу, в буквальном смысле он означает отсутствие какой бы то ни было упорядоченности. По сути, Стюарт и Голубицкий говорят об особом виде хаоса — математическом понятии, которое появилось в теории динамических систем. Идея о том, что хаос как полное отсутствие упорядоченности не существует, является частью древних верований, согласно которым есть некая общая теория, объясняющая все, будь то теогония, алхимия или наука.

ХАОС КАК ВСЕОБЩЕЕ НАЧАЛО

Поэма «Теогония» греческого автора Гесиода (VII–VIII вв. до н. э.) начинается с описания того, как появилась Вселенная из Хаоса — необозримой бездны, где беспорядочно движутся элементы всего сущего. В глубине этой изначальной бездны существовали две необъяснимые родственные сущности: Эреб (Мрак) и Нюкта (Ночь). Они отделились друг от друга и от своей матери Хаос и породили свои противоположности: Эфир (Свет) и Гемеру (День). День и Ночь объединились и образовали Время. Вслед за ними появилась Гея — элемент стабильности, праматерь, которая в столкновении с хаосом породила все сущее, затем Эрос — любовь, создатель жизни, и Тартар — преисподняя. Они не были потомками Хаоса. Гея без вмешательства мужского начала породила недостающую часть Вселенной — Уран (Небо), которое полностью накрыло ее. Пара Небо-Земля образовала симметричный и равновесный мир в Космосе.

Слово «теогония» означает «происхождение богов», а Гесиод в действительности изложил космогонию — рождение упорядоченной вселенной. Рождение богов в привычном понимании он описал позднее.

Прежде считалось, что это бюст римского философа Сенеки, но современные исследователи пришли к выводу, что перед нами изображение Гэсиода.

Несколько слов о сложности, урбанистике и лингвистике

Большинство ученых сходится во мнении с нобелевским лауреатом по физике Полем Дираком, по словам которого «физические законы должны обладать математической красотой». Ученые всегда чувствовали потребность описать всю Вселенную с помощью простой, логичной и красивой теории. Теория Платона — одна из первых, в которой материя (пять элементов) и геометрия (пять многогранников) связаны между собой. Значительно позднее за ней последовали научные и математические теории Хендрика Лоренца, Анри Пуанкаре, Германа Минковского и Альберта Эйнштейна, в которых материя и геометрия переплетались с пространством и временем.

Но если потребностью науки является нахождение всеобщего простого и красивого закона, значит ли это, что человечество в некотором роде стремится к простоте? К геометрическим фигурам относятся круг, квадрат, треугольник, пятиугольник и прочие правильные многоугольники, а также конические сечения (эллипс, гипербола и парабола), спирали и другие примечательные кривые. Эти фигуры, которые во все времена считались чистыми, божественными и очень символичными, неизменно сопровождали любую деятельность человека. Они, несомненно, являются архетипами в том смысле, который вкладывал в это слово психолог Карл Юнг. Геометрические фигуры в различных качествах применялись на протяжении всей истории человечества. Их можно проследить в архитектуре: так, форму круга имеет Стоунхендж, римские цирки и базилики; квадраты и треугольники встречаются в пирамидах и зиккуратах; пятиугольники — в декоративных элементах и так далее.

Тем не менее существуют и другие структуры. Рон Эглэш, антрополог Политехнического института Ренсселера (штат Нью-Йорк), занимался изучением архитектуры, скульптуры, рисунков на ткани, игр и других явлений культуры африканских народов. Эглэш заметил, что для разных культур характерны различные формы и шаблоны. Города Европы и Америки представляют собой сетку прямых улиц, пересекающихся под прямыми углами. Традиционные африканские поселения, напротив, имеют разнородную структуру: прямоугольные стены окружают прямоугольные участки все меньшей площади, а широкие улицы разделяются на запутанную сеть узких переулков, в которой можно увидеть сложные геометрические законы. Подобные структуры прослеживаются не только в архитектуре: их отголоски можно заметить в многочисленных и разнообразных узорах. Эглэш также обнаружил, что многие африканские поселения построены в соответствии с социальной иерархией.

Место, где будет стоять дом человека, определяется положением, которое он занимает в обществе.

Антрополог Рон Эглэш обнаружил различные типы фрактальных поселений. В их основе лежат квадраты, круги (как показано на верхнем рисунке) и т. д. В центре изображено камерунское поселение, структура которого обладает свойством самоподобия. На нижней иллюстрации приведен морфологический анализ предметов туземной культуры.

Несмотря на очевидные различия между африканскими и европейскими поселениями, обнаруженные Эглэшем, средневековые центры многих европейских городов также имеют неправильную структуру, ведь они развивались подобно живым организмам.

Эта гипотеза, основанная на теории сложности, показывает, как различные общества использовали нелинейные структуры в своей организации, чтобы поддерживать ряд внутренних взаимосвязей. Они непроизвольно имитировали динамические биологические системы. Колоннады, аркады, ряды зданий, разделенные узкими улочками, — все эти архитектурные элементы напоминают проницаемую оболочку с пустотами, через которые идет взаимообмен. Чем больше подобных сегментов (и, соответственно, пустот), тем больше информации можно передать.

План города, выстроенного по западным традициям, например Барселоны, имеет сетчатую структуру, схожую со строением живых организмов, например, крыла насекомого.

«ПЛАВИЛЬНЫЙ КОТЕЛ» ИСПАНСКИХ ГОРОДОВ

Города эволюционируют, как и живые организмы. В пространстве города, которое понимается как преобразование природного пространства и пространства деревни, образуются объекты двух различных типов: улицы (пустое пространство) и жилые районы (заполненное пространство).

Их форма и развитие по большей части обусловлены человеческим фактором. Например, испанские города развивались в соответствии с моделью, в которой можно выделить четыре периода историко-экономического развития:

— классический средиземноморский город в греко-латинской традиции;

— средневековый мусульманский и христианский город, который в эпоху Возрождения подвергся ярким и причудливым преобразованиям;

— доиндустриальный модернистский город, который затем вступил в эпоху индустриализации;

— постиндустриальный город с пригородами.

Под влиянием Востока и Запада сформировался уникальный облик современных испанских городов, непохожих на остальные европейские мегаполисы. Города Испании отличаются компактностью и древовидной структурой. В узловых элементах этих структур когда-то находились крепости, мечети, церкви и монастыри. Город в целом полностью ограничивается основным структурным элементом — городской стеной.

* * *

Когда основные процессы, происходящие в городах, меняются, можно увидеть, как изменяется исходная структура городов. Цель подобной перестройки — избежать того, что изначально было желаемым: если раньше преобладал взаимообмен между малыми группами, то теперь чаще наблюдаются большие скопления людей и высокие скорости. Чтобы не допустить коллапса, создаются кольцевые магистрали и новые районы, разбитые на квадраты. Являются ли «простые» геометрические фигуры идеальными? Будет ли подобная планировка оптимальной?

Планировка городов: только ли геометрия?

Форма городов является результатом длительного строительства, на которое влияет географическое местоположение. В процесс строительства вмешивается множество людей, принимаются решения, в результате которых появляются объекты, не подчиняющиеся евклидовой геометрии. Необходимо многомерное моделирование, то есть рассмотрение города в различных масштабах и с разных точек зрения.

Если мы посмотрим на город в разных масштабах, то увидим, что некоторые фигуры будут повторяться (итерироваться). Это доказывает, что сеть улиц города подобна ветвям дерева: и улицы, и ветви дерева формируются итеративно. Это дает основания полагать, что в этих процессах сочетаются итеративные операции и случайные события.

Структура кварталов современных западных городов отражает рациональность и порядок, на всей территории безраздельно господствует евклидова логика. Мы всегда пытаемся применить фигуры евклидовой геометрии (окружности, квадраты, кубы) к реальности, но эти фигуры — лишь математическая абстракция, следовательно, их ограничивают возможности нашего интеллекта. В итоге реальность сопротивляется подобному упрощению и упорядочиванию и восстанавливает свою сложную природу (совокупность человеческих, экономических, исторических интересов), отражая тем самым неравномерность взаимоотношений своих составных частей в различном масштабе.

Чтобы понять неравномерную, беспорядочную реальность, нужна альтернативная геометрия, в основе которой будут находиться именно эти взаимоотношения, а не идеальные геометрические фигуры.

Серия изображений структуры города, на которых заметно подобие в различных масштабах.

_{(Источник: Лаура Элизабет Виолант.)}

Геометрия и лингвистика. Знание геометрии врожденно?

Несмотря на все вышесказанное, когда нужно провести определенные границы, а территории недостаточно, то земельным участкам, как правило, придают форму прямоугольников или четырехугольников, как, например, при межевании поля перед

Кажется, что четырехугольники использовались всегда. Действительно, это одна из наиболее часто применяемых фигур наряду с кругом, спиралью и крестом. Некоторые исследователи пытались найти доказательства тому, что знания геометрии являются врожденными и не требуют знания языка или культуры. Это было подтверждено на примере племени мундуруку, живущего в Амазонии. Племя живет изолированно от нашей цивилизации на протяжении четырех сотен лет, со времени прибытия в Южную Америку европейских завоевателей. Знания геометрии, которыми владеют индейцы этого племени, доказывают, что человек обладает геометрической интуицией, которая не зависит от обучения, умения работать с картами и графическими символами и даже от наличия геометрических терминов в языке. Это открытие произвело переворот в неврологии, антропологии, психологии и герменевтике: ведь раньше было невозможно определить, необходим ли язык для познания реального мира.

В ходе современных лингвистических исследований было обнаружено, что существуют универсальные общие для всех языков семантические элементы, а также базовые языковые универсалии, характерные для устной речи. Означает ли это, что помимо одинаковых элементов языка существуют геометрические или арифметические универсалии, единые для всех людей и не зависящие от приобретенных знаний? Являются ли эти знания врожденными, унаследованными? Заложены ли они в нас генетически подобно языковым универсалиям, как утверждает выдающийся американский лингвист и философ Ноам Хомский? В 1957 г. в возрасте всего 29 лет Хомский совершил переворот в теоретической лингвистике, опубликовав работу «Синтаксические структуры». Ранее считалось, что язык, подобно любым другим навыкам, приобретается через обучение. Хомский выдвинул идею о существовании «ментального органа» языка — части мозга, благодаря которой человек обучается языку и использует его практически интуитивно. Кроме этого, он доказал, что существуют общие абстрактные принципы грамматики, присущие каждому человеческому языку, и выдвинул гипотезу о существовании универсальной грамматики.

Туземцы племени мундуруку, какими их увидел французский художник и фотограф Эркюль Флоранс в 1828 г.

Превосходство Евклида

Примерно к 323 г. до н. э. слава греческой науки распространилась по всем государствам, покоренным Александром Македонским. Неудивительно, что египетский царь Птолемей I, создав в Александрии крупный культурный центр, привлек туда афинских ученых. Евклид был назначен главой математической школы.

Первым из философов упоминает об Евклиде Прокл, согласно которому Евклид родился приблизительно в 300 г. до н. э. Относительно точности этой даты имеются сомнения, но достоверно известно, что именно Евклид систематизировал математику того времени, дополнил некоторые труды и привел неопровержимые доказательства утверждений, недостаточно подробно изложенных его предшественниками. Он обобщил и систематизировал геометрию своего времени. До Евклида математика представляла собой набор разрозненных вычислений. Благодаря его усилиям она превратилась в совокупность взаимосвязанных систем.

Греческий математик Евклид, изображенный фламандским художником Юстусом ван Гэнтом.

Известно, что Евклид написал 12 книг, из которых до нас дошли лишь пять: «Начала геометрии», «Данные», «О делении», «Явления» и «Оптика». «Начала» стали обязательными к изучению во всех университетах и научных центрах в течение следующих двух тысяч лет^[2]. Считается, что существует около полутора тысяч изданий этой книги на греческом, арабском, латыни и других языках. До середины XX века эта книга была второй по числу проданных экземпляров, уступая лишь Библии.

«Начала» — один из древнейших, красивейших и подробнейших научных трудов среди всех, что дошли до наших дней. Они состоят из тринадцати книг: шесть посвящены планиметрии, три — арифметике, одна — измерениям, три — основам стереометрии. Целью Евклида было изложить основы известной на тот момент математики без какого-либо практического применения. Его труд оказался столь совершенным, что был превзойден лишь в конце XIX века^[3]. В его теоремах все видели «истинные» подтверждения реальности, и никто не мог предположить, что возможна иная геометрия.

Чтобы попытаться понять, что побудило Евклида посвятить столько сил написанию столь подробного труда, вернемся к моменту, когда пифагорейцы обнаружили, что диагональ квадрата с единичной стороной равна √2. Это число не является рациональным, то есть его нельзя представить в виде частного целого и натурального чисел. Говоря языком той эпохи, диагональ квадрата была несоизмерима с его стороной. Этот факт сегодня кажется совершенно не удивительным, но некоторые греки, в частности пифагорейцы, считали его подлинным крахом всей математики, пошатнувшим устои космологии. Евклид, которому были известны работы пифагорейцев, стремясь найти выход из этого кризиса, решил сформулировать прочные основы всей геометрии, которые вкупе с непогрешимой логикой позволили бы получить серию непреходящих верных результатов.

Но для этого требовалось решить небольшую логическую проблему: любое доказательство основывается на одной или нескольких гипотезах, из которых путем логических рассуждений получается результат, называемый тезисом. Истинность тезиса зависит от корректности рассуждений и от истинности исходных гипотез (этот вопрос рассмотрел Аристотель в своих сочинениях под общим названием «Логика»). Чтобы иметь возможность определить истинность гипотез, нужно считать их результатами других рассуждений, гипотезы которых также должны быть истинными. Очевидно, что этот процесс бесконечен: каждая гипотеза обязательно должна являться тезисом, требующим доказательства.

Евклид понял, что не все положения в математике можно доказать, и некоторые из них нужно принять как допущения. В «Началах» он впервые использовал аксиоматический метод, что стало поворотным моментом в истории математики. Евклид рассматривал гипотезы трех типов: определения (в них приводятся значения терминов; всего Евклид формулирует 23 определения), постулаты (у Евклида их пять) и аксиомы (общие утверждения; их тоже пять^[4]).

Эта система была выстроена в соответствии с так называемым аксиоматико-дедуктивным методом, который определил путь развития всей современной математики. Бесспорно, если мы тщательно проанализируем утверждения и теоремы, которые предположительно доказаны, то обнаружим некоторые неточности. Например, Евклид использовал принцип, не указанный среди аксиом, согласно которому через две точки можно провести только одну прямую. Но эти ошибки были обнаружены лишь в начале XIX в.^[5]

Наибольшая полемика разгорелась вокруг пятого постулата «Начал», так называемой аксиомы параллельности: «В плоскости через точку, не лежащую на данной прямой, можно провести одну и только одну прямую, параллельную данной»^[6]. Этот постулат напоминает теорему, и кажется, что для него можно привести доказательство. Исследователи «Начал» и авторы комментариев понимали, что этот постулат является интуитивным.

Евклид нечасто использует его, как будто хочет избежать: впервые этот постулат используется лишь в двадцать девятой теореме. Это наводит на мысль, что сам Евклид пытался доказать это утверждение, но, убедившись в том, что это невозможно, добавил его к остальным постулатам.

Позднее это побудило математиков исправить этот «дефект» и найти доказательство пятого постулата. Безуспешные попытки продолжались двадцать веков. Тот, кто считал, что доказал этот постулат, в действительности находил другую, эквивалентную формулировку^[7]. Многочисленные бесплодные попытки привели к тому, что доказательство пятого постулата стало четвертой знаменитой задачей греческой математики после квадратуры круга, трисекции угла и удвоения куба. Лишь в XIX в. Карл Фридрих Гаусс и Николай Лобачевский окончательно показали, что этот постулат недоказуем. Это удивительное открытие поколебало уверенность в том, что геометрия Евклида является единственно возможной, и проложило путь так называемым неевклидовым геометриям, о которых мы подробно поговорим чуть позже.

Появление бесконечно удаленной прямой

В эпоху Возрождения ученые и художники начали поиски новых геометрических методов, которые бы позволили точнее изображать реальность. Среди наиболее известных — Филиппо Брунеллески, Леонардо да Винчи и Лука Пачоли, которые в своих работах стремились передать на плоскости ощущение глубины. Благодаря их усилиям сформировались практические основы науки, позднее получившей название «перспектива»^[8].

Как мы уже говорили, математика евклидова пространства является одним из ключевых элементов современной научной мысли, причем это в равной степени относится и к естественным дисциплинам, и к гуманитарным наукам и искусству. По Евклиду, математическое пространство — это пустое и абсолютное пространство, в котором формируется реальность, в том числе художественная.

В этом пространстве действуют законы перспективы, что было бы невозможно без математики Евклида, в которой описывается линейное пространство.

Фреска «Афинская школа» Рафаэля, на которой изображены практически все греческие мудрецы — известнейший пример использования перспективы. На фреске под крышей грандиозного архитектурного сооружения изображены представители классической философии, собравшиеся вместе. На этом шедевре Рафаэля время словно остановилось для мудрецов из разных эпох. И среди них наш старый знакомый Евклид. Рафаэль изобразил его в правой части картины. Евклид, согнувшись, что-то объясняет ученикам, рисуя дуги циркулем на маленькой доске. На фреске также есть и Пифагор, он сидит в противоположном углу и что-то пишет на табличке. Пифагор и Евклид изображены в разных сторонах нижней части картины — именно там, где начинаются воображаемые линии, сходящиеся к центру композиции, где расположены Платон и Аристотель. Эти линии теряются на горизонте и уходят в бесконечность.

«Афинская школа». Помимо Евклида и Пифагора, на фреске Рафаэля также изображены Зенон Китийский, Эпикур, Анаксимандр, Аверроэс, Александр Великий, Ксенофонт, Гапатия, Парменид, Сократ, Диоген Синопский, Плотин, Архимед, Заратустра, Клавдий Птолемей, Протоген и сам Рафаэль. Художник вывел себя в образе Апеллеса.

Шаг в бесконечность: проективная геометрия

Формальные принципы и основы проективной геометрии создал Жерар Дезарг (1591–1661). Этот французский математик заметил, что круг в перспективе выглядит как эллипс, а тень, которую отбрасывает на стену круглый предмет, может принимать форму круга, эллипса, параболы или ветви гиперболы в зависимости от угла наклона предмета. (Четыре упомянутые кривые — окружность, эллипс, парабола и гипербола — называются коническими сечениями.) Это означает, что проекция предмета (в нашем примере это тень) преобразует одну фигуру в другую^[9].

На основе этих наблюдений Дезарг ввел два новых понятия: бесконечно удаленную точку, называемую также несобственной точкой, и бесконечно удаленную прямую, также называемую несобственной прямой. На плоскости существует бесконечно много несобственных точек, каждой из которых соответствует свое направление. Все такие точки образуют бесконечно удаленную прямую. Аналогично в пространстве существует бесконечно много несобственных прямых, которые в совокупности образуют бесконечно удаленную плоскость. Согласно модели Дезарга, две параллельные прямые пересекаются в бесконечно удаленной точке — несобственной точке, определяемой углом наклона прямой. Иными словами, каждому углу наклона можно поставить в соответствие бесконечно удаленную точку.

Аналогично пересечением двух параллельных плоскостей будет бесконечно удаленная, то есть несобственная прямая. Следовательно, можно сказать, что две прямые, принадлежащие одной плоскости, всегда имеют общую точку (собственную или несобственную), а две плоскости пространства всегда имеют общую прямую (собственную или несобственную). Парабола будет эллипсом с несобственной точкой, гипербола — эллипсом, но уже с двумя несобственными точками. Отсюда следует принцип двойственности, который выполняется для всех теорем, устанавливающих отношение между точками и прямыми. В соответствии с этим принципом если в теореме проективной геометрии мы заменим слово «точка» на «плоскость», а слова «проходит через» — на «пересекаются в», то полученная теорема также будет верной. Благодаря этому принципу теорема «через любые две несовпадающие точки можно провести единственную прямую» имеет парную теорему: «Две несовпадающие прямые пересекаются на единственной плоскости».

Согласно новым принципам, разработанным Дезаргом, конические сечения отличаются друг от друга лишь числом несобственных точек.

Эта теория стала принципиально новой. Было нетрудно представить, что эллипс (замкнутая кривая) в перспективе будет выглядеть как окружность. Например, Дюрер точка за точкой построил все возможные сечения прямого конуса плоскостью. Тем не менее на одном из его рисунков можно увидеть, что фигура, которая в теории должна быть эллипсом, изображена в форме яйца, как будто бы Дюрер не верил своим глазам и ожидал, что по мере приближения к вершине конуса кривая будет более вытянутой по сравнению с обычным эллипсом. Напротив, казалось невозможным, что окружность в перспективе может принимать форму незамкнутой кривой с ветвями, уходящими в бесконечность, то есть форму параболы. Также казалось невозможным, что окружность в перспективе может разрываться подобно гиперболе, которая имеет две отдельные ветви.

Изображаем круглый бассейн на картине

Чтобы лучше понять, как окружность в перспективе принимает форму разных конических сечений, представим, что художник хочет изобразить на картине часть бассейна круглой формы. Художник смотрит на бассейн через воображаемое окно (именно проекцию изображения и запечатлеет на картине художник). В зависимости от угла наклона этого окна проекции будут принимать форму различных конических сечений. Мы поступим иначе: зафиксируем плоскость окна перпендикулярно полу и будем изменять положение наблюдателя и окна относительно бассейна.

Когда бассейн будет наиболее удален от окна, его проекция примет форму эллипса. Приблизим наблюдателя и окно к бассейну так, что часть бассейна будет располагаться между наблюдателем и картиной. Проекция бассейна на плоскость окна по-прежнему будет иметь форму эллипса, но часть бассейна уже не будет видна на картине, так как будет располагаться слишком низко. Поместим наблюдателя еще ближе к бассейну, так, чтобы он располагался на краю бассейна. В этом случае луч, соединяющий глаз наблюдателя и точку окружности бассейна, в которой находится наблюдатель, будет параллелен картине и никогда не пересечет ее плоскость либо же пересечет ее в бесконечно удаленной точке. Так как одна из точек окружности будет бесконечно удаленной, проекция окружности примет форму параболы.

Что произойдет, когда наблюдатель войдет в бассейн? В этом случае плоскость, проходящая через точку, в которой расположен наблюдатель, и параллельная окну, пересечет окружность в двух точках А и В. Проекциями этих точек будут бесконечно удаленные точки. Часть бассейна, которая будет располагаться позади наблюдателя, в перспективе примет форму незамкнутой кривой с двумя асимптотами. Эти асимптоты будут параллельны прямым, соединяющим наблюдателя и точки А и В соответственно. Дугу окружности, расположенную позади наблюдателя, также можно спроецировать на плоскость окна. Мы получим еще одну кривую, симметричную первой, которая будет представлять собой не что иное, как еще одну ветвь гиперболы.

Изображение круглого бассейна в зависимости от положения наблюдателя.

_{(Источник: Мария Изабель Бинимелис.)}

Открытия Дезарга позволили разработать общую теорию проекций, изучением которой занимались геометры первой половины XIX в.,среди которых отметим Гаспара Монжа и Жан-Виктора Понселе. Благодаря проективной геометрии, созданной этими математиками, стала возможной разработка неевклидовых геометрий и евклидовых моделей для них. В первых книгах о перспективе, написанных французскими исследователями начала XVII в. на основе работы Дезарга, описывалась так называемая проекция Кавалье, или военная перспектива. В 1794 г. Монж описал теорию построения ортогональных проекций трехмерных объектов на плоскости. Созданная Монжем дисциплина сегодня называется начертательной геометрией и используется при построении чертежей. В свое время начертательная геометрия в корне изменила военно-инженерное дело.

Ортогональная проекция.

_{(Источник: Лаура Элизабет Виолант)}

В архитектуре эта проекция стала использоваться значительно позже: проекция Кавалье и аксонометрическая проекция (в ней трехмерный объект изображается на чертеже при помощи проекций на три оси, находящиеся на плоскости чертежа) стали применяться в конце XIX в.

Вклад Дезарга можно вкратце описать так: в параллельной проекции эпохи Возрождения лучи зрения считались параллельными; в теории Дезарга они сходятся в бесконечно удаленной точке. Иными словами, проекция Кавалье равносильна центральной проекции, в которой взгляд художника «обращен в бесконечность». Русский художник-супрематист Эль Лисицкий полагал, что с появлением этой проекции с субъективной живописью будет покончено, так как не будет существовать точки, в которой находится наблюдатель: художник берет на себя роль творца, поскольку его взгляд исходит из бесконечности.

ПОЯВЛЕНИЕ КООРДИНАТ

Появление работ Рене Декарта и Пьера Ферма, создателей так называемой аналитической геометрии, ознаменовало начало современной геометрии. Они впервые ввели оси координат, с помощью которых точки геометрических фигур можно выразить в численном виде. Следовательно, появляется возможность использовать алгебраические методы. Таким образом, геометрические задачи сводились к алгебраическим. Решение алгебраической задачи позволяло дать ответ к исходной, геометрической задаче.

За год до публикации «Геометрии» Декарта Ферма писал: «Всякий раз, когда в заключительном уравнении имеются две неизвестные величины, налицо имеется геометрическое место, прямая или кривая».

Сумма углов треугольника

Некоторое время в механике и других областях физики геометрия занимала второстепенное положение по отношению к так называемым дифференциальным уравнениям^[10]. Это положение вещей изменил Гаусс, «принц математиков»: он заложил фундамент геометрии, в которой изучались дифференцируемые функции, иными словами, дифференциальной геометрии. Гаусс изучал кривые и поверхности в пространстве и определил базовое обозначение меры кривизны поверхности. Например, с увеличением радиуса окружности ее кривизна уменьшается. Продолжив эти рассуждения, получим, что кривизна прямой равна нулю, что и следовало ожидать.

Выполнить расчет кривизны поверхности сложнее. Если говорить упрощенно, то для двух точек данной поверхности кратчайшая кривая, соединяющая две эти точки (так называемая геодезическая линия) и не выходящая за пределы данной поверхности, будет являться кривой наименьшей кривизны. Это утверждение является более общим по отношению к постулату, который гласит, что на евклидовой плоскости кратчайшей линией между двумя точками является прямая^[11]. В такой трактовке евклидово пространство — это частный случай пространства, имеющего нулевую кривизну.

На основе этих рассуждений Гаусс доказал, что существуют поверхности, на которых сумма углов треугольников, образованных геодезическими линиями, превышает 180° либо, напротив, меньше 180°. Можно доказать, что из пятого постулата Евклида следует, что сумма внутренних углов треугольника равна 180°, поэтому открытие Гаусса противоречит пятому постулату. Судя по дневникам Гаусса, примерно в 1824 г. он пришел к следующему выводу: доказать пятый постулат, исходя из остальных постулатов, нельзя, так как он не зависит от них. Кроме того, можно создать полностью логичную геометрию, где этот постулат невыполним, и при этом не возникнет никаких противоречий с остальными четырьмя. Хотя в те годы Гаусс уже считался ведущим математиком Европы, он решил, что общество не готово к открытию такого масштаба, и не опубликовал свои записи.

Некоторые исследователи утверждают, что именно Гаусс первым рассмотрел вероятность того, что наша Вселенная имеет неевклидову геометрию. Говорят, что он поднялся на три горные вершины с теодолитом, чтобы измерить углы треугольника, образованного этими горами, но точность измерений оказалась недостаточной, чтобы сделать какие-то выводы. Любопытно, что можно экспериментально доказать, что физическое пространство не является евклидовым, но доказать его «евклидовость» не получится. Евклидовы пространства нулевой кривизны — это граничный случай, разделяющий пространства положительной и отрицательной кривизны. В измерение кривизны, как и в любое другое измерение, может вкрасться ошибка: всегда будет существовать вероятность, что отклонение от нуля слишком мало, чтобы его можно было обнаружить. Следовательно, нельзя доказать экспериментально, что данное пространство однозначно является евклидовым.

Вскоре после Гаусса еще один ученый пришел к тому же выводу, и он нашел в себе смелость опубликовать свои изыскания. В его труде пятый постулат Евклида был заменен следующим: «Через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, параллельные ей». Речь идет о геометрии Лобачевского. В действительности к этому выводу независимо друг от друга пришли два математика: Николай Лобачевский и венгр Янош Бойяи, сын Фаркаша Бойяи, друга самого Гаусса. Фаркаш Бойяи увидел в работах Лобачевского свои же идеи и настолько заинтересовался геометрией Лобачевского, что в 62 года начал изучать русский язык, чтобы прочесть его труды в оригинале. На это ему понадобилось всего несколько месяцев.

Бойяи и Лобачевский не пытались доказать пятый постулат Евклида исходя из других постулатов. Вместо этого они заметили, что постулат о параллельности прямых должен быть независимым от остальных. До них в отличие от многих своих предшественников этим же путем следовал Иоганн Ламберт. Ученые пришли к выводу, что независимость пятого постулата имеет большое значение: можно заменить его другим постулатом о параллельности прямых, возможно даже противоположным по смыслу, получить новую непротиворечивую систему постулатов и, как следствие, полностью непротиворечивую геометрию. Независимо друг от друга Бойяи и Лобачевский выбрали один и тот же альтернативный постулат и исследовали полученную неевклидову геометрию, приведя для ее теорем доказательства, аналогичные доказательствам Евклида.

АБСОЛЮТНАЯ ГЕОМЕТРИЯ

Абсолютная геометрия — это часть геометрии, которая выводится из первых четырех постулатов Евклида. Она называется абсолютной, так как является общей частью евклидовой и неевклидовой геометрий. Как мы уже показали, отличие между ними заключается лишь в пятом постулате о параллельности прямых.

Большое историческое значение имеет четырехугольник Саккери, рассмотренный Джироламо Саккери, и четырехугольник Ламберта, рассмотренный немецким математиком Иоганном Ламбертом. Они использовались для доказательства пятого постулата, но безуспешно. Саккери пытался показать, что отрицание пятого постулата ведет к противоречию, и тем самым доказать его. Однако он совершил ошибку, посчитав некоторые результаты неверными лишь на основании того, что они противоречили интуиции.

Ламберт, напротив, в посмертно изданной книге «Теория параллельных линий» (1766) приводит похожие рассуждения, что и Саккери, но не содержащие ошибок. По-видимому, он представлял, что можно сформировать геометрию без пятого постулата, так как писал: «Я склоняюсь к мысли, что гипотеза острого угла верна на некоторой сфере воображаемого радиуса». Этот немецкий математик также открыл несколько интересных формул, описывающих треугольники гиперболической геометрии, показав, что сумма углов в таких треугольниках всегда меньше 180°. По формуле Ламберта для этих треугольников справедливо следующее соотношение:

(π — (α + β + Y)) = CS_αβγ,

где

α + β + Y — сумма углов треугольника (выраженная в радианах);

С — положительный коэффициент пропорциональности, связанный с неизменной кривизной гиперболического пространства, в котором находится треугольник;

S_αβγ — площадь треугольника.

* * *

Использование нового постулата привело к созданию новой совокупности теорем и выводов, которую стали называть гиперболической геометрией. Лобачевский и Бойяи пришли к необычным выводам: через одну точку проходит бесконечно много прямых, параллельных данной; сумма углов треугольника меньше 180° для двух данных параллельных прямых существует третья прямая, перпендикулярная одной из них и параллельная другой, и так далее.

Все это противоречило интуиции: подобную ситуацию нельзя было представить, не переосмыслив понятия прямой, плоскости и другие. Тем не менее с точки зрения логики новая геометрия была абсолютно корректной. Это вызвало крупный кризис в математике XIX в., который наложился на другие противоречия той эпохи. Как бы то ни было, в трудах Лобачевского и Бойяи было окончательно показано, что постулат о параллельности прямых не связан с остальными и что Евклид совершенно справедливо включил его в число постулатов, так как его нельзя логически вывести из предыдущих.

Немного топологии

Немецкий математик Август Мёбиус (1790–1868), современник Бойяи и Лобачевского, известен благодаря ленте, носящей его имя. Чтобы сделать ленту Мёбиуса, достаточно взять полоску бумаги и соединить ее концы, повернув один из них на 180°. Если мы «пройдем» вдоль полученной поверхности, то обойдем всю ленту целиком и попадем в исходную точку, не переходя на «другую сторону», которой фактически не существует. Если мы разрежем ленту вдоль по линии, равноудаленной от краев, то получим не две ленты Мёбиуса, а одну в два раза большей длины.

Лента Мёбиуса — поверхность, соединенная «двумя сторонами».

Это приводит к удивительному результату: согласно Мартину Гарднеру, лента Мёбиуса, строго говоря, не является двумерным объектом, так как имеет определенную толщину (ведь не существует листа бумаги с нулевой толщиной). Если мы будем рассматривать ленту Мёбиуса как трехмерный объект, то увидим, что ее поперечное сечение имеет форму прямоугольника. Саму ленту в этом случае следует рассматривать как «скрученную призму». Если бы ее сечение имело форму четырехугольника, то перед тем как склеить два конца ленты, мы могли бы повернуть их друг относительно друга всего на четверть оборота, на пол-оборота (как обычную ленту Мёбиуса) или на любое другое число оборотов. А если бы ее сечение имело форму пятиугольника, а не четырехугольника? Какой объект получился бы в этом случае? Изучением подобных объектов и всех геометрических тел, которые остаются неизменными после различных преобразований, занимается область математики под названием топология, о которой мы поговорим в следующих главах.

Путешествие вокруг Гренландии. Модель Вселенной

Спустя несколько лет после открытия гиперболической геометрии, в 1851 г., немецкий математик Бернхард Риман (1826–1866), ученик Гаусса, выступил с обязательным докладом в Гёттингенском университете, чтобы получить возможность претендовать на пост приват-доцента. Этот доклад получил невероятную известность. В нем Риман обрисовал новое видение геометрии, уделив основное внимание изучению многообразий с произвольным числом измерений в различных пространствах. Используя интуитивно понятный язык и не приводя доказательств, он ввел понятие дифференцируемого многообразия (обобщение понятия дифференцируемой поверхности). Понятие «многообразие» содержит отсылку к изменяющимся координатам, которые описывают совокупность точек некоторого объекта, а прилагательное «дифференцируемое» означает, что многообразие является гладким и не содержит складок или разрывов. Согласно Риману, классические поверхности являются двумерными многообразиями, кривые — одномерными многообразиями, а точки имеют число измерений, равное нулю. Также существуют трехмерные и многомерные многообразия, которые, однако, не так просто изобразить графически.

Кульминацией первой части доклада стало определение понятия тензора кривизны, которое является обобщением понятия гауссовой кривизны на многообразиях. Кривизна кривой в точке рассчитывается путем построения соприкасающейся окружности и вычисления величины, обратной радиусу этой окружности. Так, кривизна окружности радиуса 2 во всех точках будет равна 0,5, а прямая будет иметь кривизну, равную нулю, так как соприкасающаяся окружность для этой прямой будет иметь бесконечно большой радиус.

Очевидно, что это определение непросто обобщить для всей поверхности, так как для каждой точки поверхности можно построить бесконечное множество соприкасающихся окружностей. Какую из них нужно выбрать? На этот вопрос ответил Риман, разработав так называемый тензор кривизны, причем не только для поверхностей, но и для многообразий с произвольным числом измерений.

На этой иллюстрации показано, что с увеличением кривизны радиус соприкасающейся окружности уменьшается.

_{(Источник: Мария Изабель Бинимелис.)}

Во второй части доклада Риман рассмотрел модель, которая наилучшим образом объяснила бы физическое пространство — пространство, в котором мы живем. Сколько в нем измерений? Какова его геометрия?

В трактовке Римана любое пространство (будь то плоскость, трехмерное пространство или любое другое) можно изучить с помощью дифференцируемого многообразия. Если ввести на этом многообразии понятие расстояния, или метрику, то мы определим геодезические линии (напомним, что это кратчайшие линии, соединяющие две любые точки поверхности) и геометрию на этом многообразии. Так, плоскость сама по себе не является евклидовой или неевклидовой. Лишь введение евклидовой метрики на плоскости подтверждает правильность пятого постулата Евклида, и, как следствие, плоскость становится евклидовой. Если ввести на этой плоскости другую метрику, то этот постулат, возможно, перестанет выполняться.

Например, для расчета евклидовой метрики, то есть расстояния между двумя точками с известными координатами, нужно построить треугольник: одной стороной этого треугольника будет отрезок, соединяющий данные точки, двумя другими сторонами будут проекции этого отрезка на линии, которые параллельны перпендикулярным осям координат и проходят через данные точки. Таким образом, в полученном треугольнике можно будет вычислить гипотенузу по теореме Пифагора, как показано на следующем рисунке:

Евклидово расстояние (метрика) между точками Р и Q равно гипотенузе прямоугольного треугольника, получаемого построением прямых, параллельных осям координат X, Y и проходящих через точки Р и Q. Длина искомой гипотенузы вычисляется по теореме Пифагора.

МЕТРИКА МАНХЭТТЕНА

Еще одним примером метрики, эквивалентной евклидовой метрике, является так называемое манхэттенское расстояние, рассчитываемое по формуле d((х_1,у_х), (х₂,у₂)) = |x₂ - x₁ | + |y₂ - y₁|. Эта метрика измеряет расстояние, пройденное пешеходом между двумя точками в городе, разделенном на прямоугольные кварталы. И снова мы видим, что плоскость сама по себе не является евклидовой или неевклидовой, а ее свойства зависят от используемой метрики.

* * *

Риман вновь изучил основные положения евклидовой геометрии. Проанализировав второй постулат, гласящий, что «ограниченную прямую можно непрерывно продолжать по прямой», он заметил, что это положение следует отличать от утверждения «всякая прямая является бесконечной». Он пришел к выводу, что в рамках этого нового подхода ко второму постулату необходимо отказаться от пятого постулата. Риман заменил его следующей фразой: «любые две прямые пересекаются». Путем подобных рассуждений он пришел к так называемой эллиптической геометрии.

Этот концептуальный переход будет проще понять, если мы рассмотрим геометрию поверхности Земли. Какую форму имеют кратчайшие линии, соединяющие две данные точки, то есть геодезические линии? Учтем, что они будут иметь наименьшую кривизну, а наименьшей кривизне соответствует наибольший радиус окружности. Следовательно, эти линии будут лежать на больших кругах земного шара, например на экваторе или меридиане. Этот результат, относящийся к сферической геометрии, прекрасно известен пилотам дальнемагистральных самолетов. Если самолет находится в одной точке экватора, а нужно попасть в другую точку экватора, то пилот должен следовать вдоль линии экватора. Однако если самолет находится в точке с координатой 30° северной широты, а пункт назначения находится на этой же широте, то кратчайший путь будет проходить ближе к северу. Теперь становится понятно, почему самолеты, следующие, например, из Парижа на Гавайи, летят через Гренландию, хотя Гавайи находятся южнее Парижа.

Геодезическая линия (кратчайший путь между двумя данными точками) от Парижа до Гавайских островов проходит через Гренландию и Канаду.

Чтобы найти кратчайшую линию, соединяющую две точки Земли, нужно найти плоскость, проходящую через эти точки и центр Земли, затем провести линию пересечения найденной плоскости и поверхности Земли, как показано на следующем рисунке:

Если говорить о параллельности прямых, то нетрудно заметить, что в сферической геометрии подобного понятия не существует, так как любые две «прямые» (большие круги) пересекаются. Треугольники на поверхности земного шара могут иметь два или даже три прямых угла: чтобы построить такой треугольник, достаточно поместить две его вершины на экваторе, а третью — на одном из полюсов. В отличие от евклидовой геометрии, где все треугольники имеют сумму углов, равную 180°, в гиперболической и сферической геометрии все обстоит совершенно иначе. В сферической геометрии сумма углов треугольника всегда больше 180° и различается у разных треугольников. В одних треугольниках она может быть равной 190°, в других — 250°. Однако доказано, что два треугольника одной и той же площади имеют равную сумму углов.

Треугольник, построенный на поверхности сферы. Сумма углов этого треугольника больше 180°.

ГЕОМЕТРИЯ ПРОСТРАНСТВА

Какая из трех геометрий «настоящая»? Какая из трех геометрий, о которых мы рассказали выше, лучше описывает реальный мир? Со временем стало понятно, что геометрия Евклида является полностью приемлемым приближением реальности, если речь идет об объектах, сопоставимых по масштабу с Землей, но на больших расстояниях все уже не столь очевидно. Если мы попробуем измерить расстояния на поверхности сферы и найти кратчайшие расстояния на ней, то поймем, что наш мир описывается эллиптической геометрией (геометрией Римана). При путешествиях со скоростями, близкими к скорости света, пространство-время будет описываться геометрией Минковского, которая является неевклидовой. Но что происходит во Вселенной вдали от поверхности Земли, если не брать в расчет время? Действительно ли мы живем во вселенной, пространство которой подчиняется законам геометрии Евклида?

Гаусс по просьбе короля Ганновера некоторое время занимался геодезическими исследованиями. В ходе исследований ему потребовалось измерить углы треугольника, образованного тремя горными вершинами, отстоящими друг от друга на расстояние около 50 миль. Отклонение полученной суммы углов от 180° было меньше допустимой ошибки измерений; таким образом, найденная сумма углов треугольника соответствовала всем трем гипотезам. В свою очередь, Лобачевский заметил, что треугольник, вершины которого расположены на Земле, будет слишком мал, чтобы заметить расхождения с евклидовой геометрией. Лобачевский занялся астрономическими исследованиями, но ему также не удалось прийти к какому-либо выводу, так как разница при измерении расстояний между Землей и Солнцем составила менее одной тысячной секунды. Тогда он обратился к треугольникам большего размера и занялся наблюдениями параллакса звезд. Однако ни ему, ни кому-то другому не удалось найти треугольник, где сумма углов отличалась бы от 180°, несмотря на то что в гиперболической геометрии эта разница возрастает с увеличением площади треугольника.

Согласно теории относительности, нашу Вселенную наилучшим образом описывает эллиптическая геометрия (геометрия Римана). Б. Льюис говорил: «В общей теории относительности Эйнштейна геометрия пространства — это риманова геометрия. Свет движется вдоль геодезических линий, а кривизна пространства зависит от природы материи, его составляющей».

Эрлангенская программа. Что же такое геометрия?

Для утверждения в должности профессора факультета философии и члена совета Эрлангенского университета Феликс Клейн (1849–1925) в 1872 г. написал доклад (правда, он так и не был зачитан публично), который можно считать одним из ключевых трудов по геометрии наряду с диссертацией Римана и «Началами» Евклида.

В своем докладе Клейн попытался дать формальное определение геометрии, выйдя за рамки интуитивных представлений. Он систематизировал множество появившихся в то время разделов геометрии в так называемой эрлангенской программе, где привел их классификацию в зависимости от свойств, которые остаются неизменными для определенных групп преобразований^[12]. Понятие группы было известно до Клейна, но именно он открыл фундаментальную взаимосвязь геометрии и групп преобразований. Так, евклидова геометрия изучает свойства фигур и тел, которые не изменяются при движениях без деформации. К подобным движениям, которые называются изометрическими преобразованиями (в переводе с греческого «изометрия» означает «равного размера»), относится перенос, симметрия, вращение и их композиции. Инвариантами этих преобразований являются, к примеру, расстояние между точками, площадь поверхности, углы между прямыми и так далее.

Аналогично аффинная геометрия изучает свойства фигур, инвариантные относительно аффинных преобразований (к ним относятся изометрические преобразования, растяжения и сжатия). Проективная геометрия изучает свойства, инвариантные относительно группы проекций, топология занимается изучением инвариантов непрерывных преобразований.

Помимо прочего, Клейн доказал, что евклидову геометрию, аффинную геометрию и неевклидовы геометрии можно считать частными случаями проективной геометрии. Если не вдаваться в детали, то доказательство основано на рассмотрении преобразований проективного пространства, которые оставляют неизменным определенное коническое сечение, называемое абсолютным. В зависимости от типа конического сечения результатом будет тот или иной раздел геометрии.

Если оставить в стороне технические вопросы, то это утверждение приводит к очень важному результату: геометрия Евклида является согласованной (непротиворечивой) тогда и только тогда, когда непротиворечивыми являются неевклидовы геометрии. Так был положен конец спорам о том, имеют ли смысл неевклидовы геометрии. Тем не менее еще несколько лет вопрос оставался открытым, так как некоторые исследователи считали рассуждения Клейна ошибочными.

Эрлангенская программа открыла путь к изучению абстрактных геометрических пространств. Теперь математики могли не ограничиваться фигурами на плоскости или в трехмерном пространстве. Стало возможным изучать множество измерений и переменные, которые не обязательно являются пространственными. Например, можно говорить о пространстве переменных термодинамики, описывающих состояние газа, которое может иметь больше трех измерений: давление, объем, температуру и различные концентрации веществ, из которых состоит газ. Мы можем изучать геометрические свойства этих переменных, но уже с абстрактной точки зрения.

О частичке пыльцы и геометрии в природе

Если мы попытаемся описать Вселенную с помощью фигур, которые изучал Евклид, то столкнемся со множеством ограничений. Фигуры геометрии природы очень далеки от идеальных фигур евклидовой геометрии.

В начале XIX в. шотландский ботаник Роберт Броун исследовал каплю жидкости, которая осталась в магматической породе при ее затвердевании. Изучив каплю под микроскопом, Броун увидел следы мельчайших частиц, которые безостановочно совершали абсолютно хаотичные колебания. Он уже наблюдал подобное движение, когда изучал движение частичек пыльцы в воде. Броун дал этому явлению такое объяснение: жизненная сила молекул растения сохранилась спустя много лет после его смерти. Однако впоследствии это объяснение было признано неубедительным. Броун начал склоняться к мысли, что подобные колебания, получившие название броуновского движения, имеют физическую, а не биологическую природу. Например, с уменьшением размеров частиц или с ростом температуры скорость движения частиц увеличивалась.

Лишь в 1905 г. Альберт Эйнштейн изучил броуновское движение с точки зрения кинетической теории газов, разработанной Джеймсом Клерком Максвеллом и Людвигом Больцманом. В наши дни это явление объясняется следующим образом: частица пыльцы, погруженная в жидкость, соударяется с молекулами жидкости, и при каждом соударении траектория частицы изменяется. С одной стороны, отклонения ее движения произвольны, с другой стороны, так как микроскоп позволяет увидеть только колебания определенной величины, истинная траектория частицы намного сложнее наблюдаемой.

Броуновское движение стало одним из первых явлений природы, в котором прослеживаются признаки самоподобия в различном масштабе. На рисунке приведена траектория броуновской частицы, зафиксированная в 1912 г. французским физиком Жаном Батистом Перреном. Положение частицы фиксировалось каждые 30 с.

Графическое изображение броуновского движения частицы. Можно оценить сложность траектории и ее самоподобие в различных масштабах. На нижней иллюстрации приведено увеличенное изображение траектории движения между точками А и В верхнего изображения.

Строго говоря, траектория броуновской частицы не отражает физическую действительность. Положение частицы фиксировалось каждые 30 с и обозначалось точкой, затем эти точки соединялись прямыми. Следовательно, физическую действительность отражают только точки, которые обозначают положение броуновской частицы по прошествии определенного промежутка времени. Так, если мы рассмотрим две соседние точки А и В, будем обозначать положение частицы с интервалом не в 30 с, а в 0,3 с и будем соединять полученные точки прямыми, то снова получим ломаную линию той же сложности, но меньших размеров. Можно выбрать еще меньший интервал, например 0,003 с, но и в этом случае ситуация принципиально не изменится. Траектория броуновской частицы имеет одинаково сложную структуру вне зависимости от выбора временного интервала наблюдений.

Интересно, что этот факт заметил еще Перрен в 1906 г. В частности, он обратил внимание на то, что для выбранной точки траектории броуновской частицы нельзя провести касательную, и отметил:

«Говоря языком геометрии, кривые, не имеющие касательных, могут считаться правилом, в то время как правильные кривые — такие, например, как окружность, — любопытным, но весьма частным случаем.

<…> Те, кто впервые слышит о кривых без касательных, часто склонны полагать, что в природе не существует ни подобных сложных конструкций, ни даже намека на них.

Не покидая экспериментально подтверждаемой реальности, мы наблюдаем под микроскопом проявление броуновского движения на примере малой частицы, взвешенной в толще жидкости. Мы видим, что направление прямой, соединяющей точки, соответствующие двум очень близким во времени положениям частицы, изменяется по мере уменьшения временного промежутка между двумя измерениями совершенно беспорядочно. Беспристрастный наблюдатель заключит из этого, что он имеет дело с кривой, к которой нельзя провести касательную».

Комментарий Перрена остался без внимания, и этим вопросом никто не занимался до конца 1960-х годов, когда французский и американский математик Бенуа Мандельброт вновь поднял эту тему. Если бы исследователи уделили больше внимания наблюдениям Перрена в начале века, то фундамент нового раздела геометрии был бы заложен на шесть десятилетий раньше.

Бенуа Мандельброт родился в Польше в 1924 г. в семье литовских евреев и в 1936 году эмигрировал во Францию, где поселился его дядя Шолем — один из участников и основателей группы Бурбаки^[13]. Члены группы Бурбаки, в частности, отрицали возможность применения геометрических фигур и графиков для иллюстрации понятий или доказательств: они считали, что зрение может обманывать разум.

В 1945 г. дядя порекомендовал Бенуа ознакомиться с 300-страничной рукописью французского математика Гастона Жюлиа под названием «Записка о приближении рациональных функций». В соответствии с идеями школы, членом которой он являлся, Шолем Мандельбройт посоветовал племяннику забыть о геометрии. Мандельброт не последовал совету дяди, хотя и обратился к рукописи лишь в 1970 г., когда с помощью компьютеров в исследовательском центре IBM имени Томаса Джона Уотсона получил иллюстрации, удивившие научное сообщество высоким уровнем детализации. Позднее эти иллюстрации стали называться множествами Мандельброта.

Вместе со своими предшественниками Мандельброт вывел на передний план в математике и естественных науках новую дисциплину, которая приобрела огромное значение. Этой дисциплиной была фрактальная геометрия.

«Фрактальная геометрия заставит вас на все смотреть другими глазами. Дальше читать опасно. Вы рискуете потерять свое детское видение облаков, лесов, галактик, листьев, перьев, цветов, скал, гор, бегущих ручьев, ковров, кирпичей и многого другого. Ваше восприятие этих вещей никогда больше не будет прежним».

Так начинается книга «Фракталы повсюду» (Fractals Everywhere) английского математика Майкла Барнсли, профессора Австралийского национального университета и знаменитого исследователя в этой области. По его мнению, фрактальная геометрия — это прежде всего новый язык. Следуя аналогии между геометрией и лингвистикой, приведенной в разделе этой книги об урбанистике, и используя метафору, придуманную исследователями Хартмутом Юргенсом, Хайнцем-Отто Пайтгеном и Дитмаром Заупе, рассмотрим некоторые фундаментальные свойства этого раздела геометрии.

Алфавит западных языков (например, латыни) имеет ограниченное число символов. В восточных языках, например в китайском, количество различных символов огромно. В западных языках слова, имеющие смысл, образуются путем сочетания букв. В языках Востока, напротив, символы сами по себе обладают значением. Аналогично западным языкам традиционная геометрия (например, евклидова или риманова) оперирует немногочисленными элементами, в частности прямыми, окружностями и так далее. С их помощью создаются другие, более сложные конструкции, обладающие определенным смыслом в зависимости от контекста.

Фрактальная геометрия, напротив, соответствует семейству восточных языков в том смысле, что ее элементы сами по себе имеют смысл и отличаются от объектов традиционной геометрии. Каковы же эти элементы? Проще всего определить их с помощью правил вычислений или алгоритмов, которые можно считать значимыми единицами языка фракталов. Алгоритмы — это правила и инструкции построения конкретных фигур, для выполнения которых часто требуется прибегать к помощи компьютера.

С этой точки зрения классическая геометрия является первым приближением структуры физических объектов. Подобные объекты с очень высокой степенью точности описывает дифференциальная геометрия. Например, наблюдатель, находящийся на Земле, может убедиться, что сфера является адекватной моделью для Луны. Тем не менее для астронавта, который находится поблизости от Луны и может наблюдать кратеры на ее поверхности, подобная модель уже не будет корректной. Смоделировать сложные и нерегулярные окружающие нас структуры с помощью традиционных приемов очень сложно. Фрактальная геометрия в некотором роде заполняет собой этот промежуток. Ее можно использовать, чтобы с точностью описать очертания как листа дерева, так и всего дерева целиком.

Фракталу сложно дать общее определение, поскольку многие из них неприменимы ко всем существующим семействам фракталов. Возможно, лучшим способом будет указать общие черты математических процессов, результатом которых являются фракталы. В конечном итоге наиболее интересной чертой фракталов и основой их фундаментальных математических свойств являются отличительные особенности процессов, порождающих фракталы.

Так, фрактал формируется как результат бесконечного числа итераций (повторений) четко определенного геометрического преобразования. Это преобразование, как правило, очень простое и определяет итоговый вид фрактала. Благодаря тому что эта процедура повторяется бесконечное число раз, ее результатом будут внешне чрезвычайно сложные структуры.

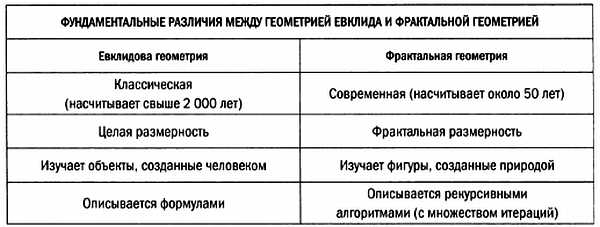
Во фрактальной геометрии сложная фигура может получаться в результате удивительно простого процесса. Верно и обратное: не следует недооценивать возможные результаты простого процесса, часто они могут оказаться весьма сложными.

Основная мысль Мандельброта такова: многие природные объекты (горы, облака, побережья, капилляры) на первый взгляд невероятно сложны, но в действительности обладают одним и тем же геометрическим свойством — неизменностью в различных масштабах.

В 1975 г. Мандельброт опубликовал книгу «Фрактальные объекты: форма, случайность и размерность» в которой объясняется, что неологизм «фрактал» происходит от латинского fractus («сломанный, разбитый»). Позднее американский автор научно-популярных книг Джеймс Глейк в книге «Хаос. Создание новой науки» рассказал, что одним зимним вечером Мандельброт работал над книгой и задумался над тем, какое название можно дать фигурам, размерности и всему разделу геометрии, который описывался в книге. Он начал бегло пролистывать латинский словарь. Прилагательное fractus, происходящее от глагола frangere («ломать»), и звучание родственных ему английских слов fracture («излом»), fraction («обломок») показались подходящими. Так он придумал новое слово — фрактал.

В 1982 г. он публикует новую книгу «Фрактальная геометрия природы» с удивительными иллюстрациями, созданными при помощи компьютерных технологий. На 15-й странице первого издания этой книги Мандельброт предлагает определение, но сам же и уточняет, что оно не охватывает отдельные множества, которые по разным причинам также относятся к категории фракталов. Его определение звучит так: «Фрактал — это множество, хаусдорфова размерность которого строго больше его топологической размерности». (Более подробно об этих и других видах размерности будет рассказано в главе 2, стр. 67.)

Были предложены и другие определения. По сути, для этого понятия до сих пор не существует ни точного определения, ни единой общепринятой теории.

Мандельброт не изобрел фракталы — они всегда существовали и «ждали», пока кто-то обратит на них внимание и раскроет их тайны. Они были незримыми спутниками человека с самого начала, подобно хаосу, ставшему невидимой «рукой, качающей колыбель», которая, согласно английской поговорке, и правит миром. Мандельброт умер в Кембридже 14 октября 2010 г.

Глава 2 Неизвестное измерение. Составление карты Вселенной

Блох больших кусают блошки,

Блошек тех — малютки-крошки.

Нет конца сим паразитам,

Как говорят, ad infinitum.

Джонатан Свифт. О поэзии. Рапсодия (1733)

В 1904 г. в Голландии появились упаковки какао-порошка, на которых было нанесено любопытное повторяющееся изображение. Это был не первый случай, когда художник обращался к подобному эффекту. За много лет до этого, в 1320 г., Джотто использовал этот прием в изображении алтаря на «Триптихе Стефанески». Но на эту особенность картины обратили внимание лишь по прошествии многих лет. В 1970 г. голландский журналист написал об этом художественном приеме статью и использовал для него название «эффект Дросте», ссылаясь тем самым на марку какао-порошка.

Вселенная в капле воды

На этой пачке какао изображена медицинская сестра с подносом в руках, на котором находятся два предмета. Они привлекают наше внимание как раз потому, что на них снова изображена та же медсестра в той же позе и так далее, пока наши глаза способны различить мельчайшие детали. Если бы мы каким-то образом попали на одну из этих этикеток, то смогли бы увидеть всё так, как будто бы находились снаружи. Мы могли бы узнать, на какой этикетке находимся, только если бы наше тело не изменилось в размерах.

Здесь речь идет о частичном самоподобии. Это свойство называется самоподобием, так как малые изображения подобны большому, и частичным, поскольку большое изображение не состоит исключительно из повторяющихся малых. Для полного самоподобия необходимо, чтобы при увеличении любой части изображения его покрывало множество копий одного и того же портрета медсестры.

Рекурсивное изображение на этой упаковке какао дало название эффекту Дросте.

Рассмотрим известный рисунок, на котором большая рыба съедает маленькую. На первый взгляд кажется, что здесь мы имеем дело с тем же видом самоподобия, что и на упаковке какао: на рисунке изображено бесконечное множество маленьких рыб, каждая из которых хочет съесть еще более мелкую. Однако если мы увеличим любую часть изображения, то увидим, что на каждой чешуйке каждой рыбы также изображено множество крошечных рыбок, которые гонятся друг за другом. Здесь речь идет о полном самоподобии, которое обеспечивается за счет применения 11 различных функций. Каждая функция превращает большую фигуру в другую, меньшего размера, повернутую и (или) смещенную, которая затем помещается на общее изображение. Таким образом, на первом шаге поверх большой рыбы помещается одиннадцать более мелких изображений. Подобные функции можно применять до бесконечности, и в результате все изображение будет представлять собой коллаж.

Функции этого типа описал Барнсли, который доказал так называемую теорему коллажа. Позднее мы подробно расскажем о том, как создаются подобные функции, и узнаем, как благодаря теореме работает этот метод построения фигур.

Первая итерация изображения, на котором большая рыба съедает маленькую.

Третья итерация этого же изображения.

Финальная итерация.

_{(Источник иллюстраций: Мария Изабель Бинимелис и Лаура Элизабет Виолант.)}

По всей видимости, первые представления о рекурсивности и самоподобии появились в XVII веке благодаря разностороннему немецкому мыслителю Готфриду Вильгельму Лейбницу. Он упоминает схожие понятия как минимум дважды. Лейбниц так объяснил другу задачу об укладке фигур: «Представь себе круг, в который вписаны три равные окружности наибольшего радиуса. Последние могут содержать в себе три вписанных окружности каждая и так далее». Здесь также виден интерес Лейбница к задачам упаковки фигур, которые неизменно сохраняли популярность благодаря своему широкому применению.

Возможно, самой известной из подобных задач является гипотеза, предложенная Кеплером. Она гласит, что оптимальной укладкой пушечных ядер (такой, при которой они занимают минимально возможный объем) является пирамида, подобная тем, что выстраивают на прилавках торговцы фруктами. Эта на первый взгляд простая гипотеза была полностью доказана лишь в 2005 г. с помощью компьютера. Большая часть задач об упаковке берет начало в физике и биологии, применяется множеством способов в кристаллографии, при изучении структуры аморфных материалов и коллоидных растворов. Даже задача об оптимальной передаче цифровых сигналов может быть изложена как вариант задачи об упаковке сфер — так называемой задаче о контактном числе.

Во втором случае Лейбниц сказал, что капля воды содержит целую вселенную, которая, в свою очередь, также содержит более мелкие капли воды, каждая из которых вновь содержит в себе вселенную и так далее. Однако эта идея и многие другие, схожие с ней, со временем были отвергнуты, так как их нельзя было подтвердить экспериментально. Сегодня мы можем констатировать, что подобные рассуждения не столь нелепы, как может показаться. Было высказано множество идей о схожести модели атома Нильса Бора, где вокруг ядра по орбитам вращаются электроны, с законами вращения планет Кеплера. Здесь также прослеживается связь между микрокосмосом и макрокосмосом. Хотя нам известно, что эти модели совпадают не полностью, не стоит быть уверенным в том, что современные модели наилучшим образом отражают реальность. Возможно, что идеальной модели не существует, и мы будем вынуждены вечно довольствоваться лишь все более и более точными приближенными моделями.

Оставим встороне эти метафизические вопросы и добавим, что сегодня известно множество объектов, которые содержат сами себя. Некоторые были описаны в теории, другие встречаются в природе. Самоподобием обладает множество событий и явлений, что будет показано в следующих главах. Хотя обнаружить самоподобные предметы несложно, практически не существует автоматизированной процедуры генерации рекурсивных функций, которые бы описывали подобные предметы.

Вселенная внутри круга

Тот факт, что самоподобие и рекурсивные или итеративные события столь тесно связаны, может вызвать в нас странное чувство. Его попробовал выразить американский художник Дуэйн Майкл в своей серии фотографий Things are Queer («Странные вещи»). Человеческий разум притягивают бесконечные процессы. Они толкают нас на эксперименты с бесконечностью — недостижимой и влекущей. Возможно, подсознательно, а быть может, и нет, в этих поисках художники предлагают нашему вниманию столько же, сколько и ученые.

Серия фотографий Things are Queer Дуэйна Майклса.

Художник Мауриц Эшер, голландец (вспомним, что знаменитая этикетка с упаковки какао была также нарисована в Голландии), использует этот же эффект Дросте в своем шедевре «Галерея гравюр». Эту связь подтверждает и сам Эшер: «Юноша слева смотрит на гравюру, на которой изображен он сам». Но мы никак не можем это проверить, потому что именно в том месте, куда обращен взгляд юноши, находится подпись художника на белом круге. Это слепое пятно всегда было загадкой. Сам Эшер говорил, что «там все настолько детально, что продолжать было бы невозможно». Какую загадку скрывает этот ореол? Что мы увидели бы, если бы Эшер продолжил рисовать в соответствии с общим сюжетом гравюры? Говоря о сюжете, мы имеем в виду сеть линий, которые соответствуют горизонталям и вертикалям на рисунке без деформаций. Например, эту сеть частично формируют линии, образующие «вертикальные» и «горизонтальные» стороны картин и окон.

То, что на самом деле находится за первой аркой, стало известно лишь в 2000 г., когда Хендрик Ленстра, соотечественник Эшера, проанализировал эту сетку линий. Сначала он восстановил «Галерею гравюр» без искажений, и в центре картины появился пустой участок в форме бесконечной спирали. Затем он заполнил этот участок на основе имеющихся частей картины.

Слева — «Галерея гравюр», справа — ее неискаженное изображение.

_{(Источник: Notices of the AMS, том 50, номер 4.)}

Бруно Эрнст, изучавший картину Эшера, так описывает последовательность увеличенных изображений неискаженной картины: «Юноша смотрит на гравюры Эшера в галерее искусств, и его взгляд падает на гравюру, очень похожую на гравюру „Сенгела, Мальта“ 1935 года. Юноша внимательно смотрит в верхний правый угол, где можно увидеть часть полуострова Сенгела. Там он замечает строение с навесом, очень похожее на галерею искусств, куда он только что вошел. Если мы уделим пристальное внимание деталям, то увидим, что в галерее представлены работы Эшера, и даже можно увидеть юношу, который рассматривает гравюру с тем же видом Мальты».

Последовательное увеличение неискаженного рисунка.

_{(Источник: «Эффект Дросте и „Галерея гравюр“ Эшера», Бруно Эрнст.)}

На основе математического описания сетки линий и выпрямленного рисунка Ленстра создал компьютерную программу, с помощью которой узнал, что же находится внутри таинственного ореола, и пошел дальше, чем Эшер… до бесконечности. Слепое пятно исчезло, и оказалось, что в центре «исправленной» версии «Галереи гравюр» вся картина повторяется бесконечное число раз. Любопытнее всего то, что сетку линий до самого центра можно было продолжить, даже не располагая исходным изображением внутри спирали.

Увеличенное изображение центральной части полной версии литографии.

_{(Источник: «ЭффектДросте и „Галерея гравюр“ Эшера», Бруно Эрнст.)}

Эшер был прав, когда говорил, что заполнить центральный круг невозможно, так как нужно работать с бесконечно большой точностью. Однако с помощью анимации можно передать всю информацию, которая содержится на картине.

То, как Эшер манипулировал пространством, делая это интуитивно, руководствуясь эстетическими принципами, необычно для мира искусства. Он использовал отражения, растяжения, деформации, проекции и другие аналогичные преобразования, с помощью которых скрывал в своих произведениях новые сложные миры.

Название этого раздела «Вселенная внутри круга» содержит отсылку к шедевру «Галерея гравюр», в центральном круге которого вся картина повторяется снова и снова, закручиваясь в бесконечную спираль. Оно также говорит о группе базовых элементов, которые использовал Эшер для бесконечного замощения центральной круговой области картины.

Фактически все картины Эшера можно разделить на три типа. На картинах первого типа изображены пейзажи и сцены из повседневной жизни, представленные с необычных ракурсов. На картинах второго типа мы видим невозможные фигуры и сооружения. К третьему типу относятся гравюры, на которых вся плоскость или ее часть раскалывается на части.

Покрытие поверхности мозаикой, в основе которой лежит цикличность и различные виды симметрии, создает ощущение бесконечности. Эшер упорно хотел изобразить бесконечность и был недоволен тем, что холст картины ограничивает его в этом. Он искал способ изобразить бесконечность в конечном пространстве и с этой целью начал создавать фигуры, покрытые сетчатым узором из кругов и квадратов.

Он стал рисовать серии повторяющихся фигур, вложенных одна в другую, начиная с края круглого или квадратного холста. По мере приближения к центру фигуры уменьшались в размерах. Тем не менее похоже, что и этим приемом он остался недоволен.

В 1958 г. он ознакомился со статьей британского ученого Гарольда Коксетера под названием Cristal Symmetry and Its Generalizations («Симметрия кристаллов и ее обобщения»), где описывался оригинальный способ укладки плиток, который вдохновил Эшера на новые поиски. Речь шла о разбиении круга на треугольники так, что их число возрастало по мере приближения к краю.

Этим рисунком Коксетер иллюстрировал модель неевклидова метрического пространства, называемого диск Пуанкаре. Диск Пуанкаре является моделью геометрии Лобачевского, в которой через одну точку можно провести несколько прямых, параллельных данной, о чем мы рассказывали в прошлой главе.

Диск Пуанкаре является частью важного ряда моделей геометрии Лобачевского, так как в реальном трехмерном пространстве (на языке математики оно обозначается ) не существует поверхности, на которой бы выполнялись законы этой геометрии^[14]. Следовательно, этот раздел геометрии отличается от эллиптической геометрии, прекрасной моделью которой является сфера.

Модель, описанная Пуанкаре, — это круг, метрика которого отличается от метрики евклидовой плоскости. Метрика диска Пуанкаре такова, что все уменьшается в размерах по мере приближения к границе круга^[15]. Как следствие, человек, живущий в мире Пуанкаре, никогда не сможет попасть на «край света».

ОБИТАТЕЛИ ГИПЕРБОЛИЧЕСКОГО МИРА

Понимают ли существа, обитающие в мире Пуанкаре, в каком пространстве они живут? Представим, что один из обитателей этого мира измерил длину свой ладони, которая оказалась равной 20 см. Затем он начинает идти в сторону края круга и спустя некоторое время снова измеряет длину ладони. Для нас его ладонь уменьшится в размерах, а для него длина ладони будет по-прежнему равна 20 см, так как расстояние между делениями линейки тоже уменьшится. Измерения относительны: для нас, сторонних наблюдателей, его ладонь уменьшится в размерах, для жителя этой плоскости ее длина не изменится. Аналогично для нас его мир ограничен, а для него — безграничен, так как он никогда не сможет достичь его края. Как обитатель этого мира может понять, что живет на гиперболической плоскости? Один из возможных способов — найти сумму углов произвольного треугольника, которая будет меньше 180°. Треугольник должен быть достаточно большим, чтобы на результат не повлияла погрешность измерений, так как с увеличением размеров треугольника сумма его углов будет уменьшаться. Еще один способ — провести окружность радиуса r и убедиться, что ее длина превышает 2πr (поэтому плоскость и называется гиперболической). Однако в этом случае радиус окружности также должен быть достаточно большим.

* * *

В серии работ «Предел — круг» Эшер попытался изобразить эту метрику и свойство прямых в гиперболической геометрии, в то же время дав собственную трактовку бесконечности как вселенной в капле воды. Схемы замощения могут отличаться: представленная на рисунке схема, которую использовал в своей работе

Пуанкаре, состоит из семиугольников. Каждая вершина семиугольника является общей еще для двух семиугольников. Особенный интерес представляет картина Зшера «Ангелы и демоны», на которой пятиугольники, в которых все углы «прямые», каждой вершиной соединяются еще с тремя.

Слева — треугольная функция, которую использовал Пуанкаре в работе об эллиптических функциях. Как позднее говорил сам Пуанкаре, в этой работе он применил неевклидову геометрию. Справа — «Ангелы и демоны» Эшера.

О войнах и длине границ

Чешский географ и статистик Яромир Корчак изучал влияние географического местоположения на население. В 1938 г. он провел статистические исследования числа больших островов в разных регионах мира и обнаружил закон, который сыграл ключевую роль в определении понятия размерности в математике. Для данной площади S он вычислил число островов с площадью, большей чем S. Подсчитав по этому правилу число островов N(S) для каждого S, он представил результаты в виде точек на оси координат. Выполнив эти действия для разных регионов, для каждого из них он получил соответствующий график. Он заметил, что эти графики похожи: N обратно пропорционально S в определенной степени, то есть N равно константе k, разделенной на S в степени, которую мы обозначим за D:

N(S) = k/S^D.

Корчак сопоставил каждому региону соответствующее значение D. Впоследствии его результаты были уточнены, и теперь нам известно, что D для Африки (где один большой остров окружен мелкими) равно 0,5; D для Индонезии и Северной Америки (где крупные острова преобладают не столь явно) равно 0,75, а для всей планеты это число равно 0,65.

В прошлом веке многие ученые выявили похожие законы, например для словарного запаса людей или уровня воды в Ниле. Во всех этих законах фигурирует показатель степени, схожий с D. Наиболее значимым из них является закон, открытый Льюисом Фраем Ричардсоном (1881–1953), английским ученым и пацифистом, который первым применил современные математические методы для прогнозирования погоды, а также для изучения причин возникновения войн и их предотвращения. Изучая закономерности возникновения войн, он решил исследовать взаимосвязь вероятности войны между двумя странами и протяженности границы между ними.

Много лет Ричардсон собирал данные о протяженности границ между странами, но результаты его исследований были опубликованы лишь в 1961 г., спустя восемь лет после его смерти. В своей статье он отметил, что разные страны приводят разную длину одних и тех же границ с другими странами (для этого было достаточно обратиться к соответствующим справочникам). Например, в испанских справочниках длина границы между Испанией и Португалией равна 987 км, в португальских — 1214 км. Аналогично в голландских источниках указана длина границы с Бельгией в 380 км, в бельгийских источниках приведена цифра в 449 км.

НАСКОЛЬКО ВЕЛИКА СПИРАЛЬ?

Спирали представляют собой класс объектов, которые ставят под сомнение традиционный способ измерения длины. Спиралями интересовались математики всех времен. Так, Архимед написал трактат о спиралях и открыл особый тип спиралей, который был назван в его честь. Архимедова спираль подобна поперечному сечению свернутого ковра, то есть расстояние между ее витками всегда остается постоянным. Спираль Архимеда описывается следующей формулой: r = qφ, где r — координата точки спирали, которая зависит от угла φ поворота центральной оси против часовой стрелки (в радианах), a q — константа, которая при умножении на 2π дает расстояние между последовательными витками спирали. Еще одним видом спирали является логарифмическая, представленная на рисунке ниже:

Для этой спирали произведение константы q на угол φ дает не r, а логарифм r. Швейцарский математик Якоб Бернулли был настолько впечатлен подобием всей спирали и любой ее части (то есть самоподобием), что повелел написать на своем надгробии такие слова: Eadem Mutata Resurgo, что в переводе означает «измененная, я вновь воскресаю». Точнее говоря, свойство, которым восхищался Бернулли, заключается в том, что сжатие или растяжение этой спирали равносильно ее повороту на определенный угол.

Рассмотрим любопытный пример двух многоугольных спиралей, подобных тем, что показаны на рисунке выше. Справа изображена бесконечная спираль. В ней каждая сторона относится к предыдущей как 1/q. Сумма длин всех сторон равна сумме ряда 1 + 1/q + 1/q² + 1/q³ +…, равной q/(q — 1). Следовательно, эта спираль имеет конечную длину. Например, если мы выберем q = 1,05, сумма (то есть длина всех сторон) будет равняться 21.

Спираль слева построена по иному, но тоже очень простому правилу: большая сторона спирали равна 1, следующая — 1/2, следующая — 1/3, затем 1/4 и так далее. Известно, что этот ряд не сходится, то есть спираль на рисунке слева имеет бесконечную длину, а спираль на рисунке справа — конечную длину. Можно ли было предположить что-то подобное?

* * *

На основе графиков Ричардсон попытался выяснить причину столь заметных различий, которые могут достигать 20 %. Его объяснение столь же удивительно, сколь и очевидно: единица измерения, используемая одной страной, может быть намного меньше, чем единица измерения, применяемая в другой стране. В чем же заключались эксперименты Ричардсона? Допустим, мы фиксируем раствор циркуля, равный 10 см. Затем мы с помощью циркуля по карте измеряем протяженность береговой линии, непрерывно отсчитывая ее длину. Полученное значение является лишь приближенным, так как береговая линия на карте имеет выпуклости и вогнутости размерами меньше 10 см. Затем уменьшим раствор циркуля и установим его равным 1 см, после чего повторим измерения. Очевидно, что в этот раз результат измерений будет больше, так как ломаная линия, прочерченная циркулем, будет точнее соответствовать береговой линии. Здравый смысл подсказывает, что эти значения сходятся к некоторому конечному числу, которое и будет истинной длиной побережья или границы. Однако Ричардсон показал, что результат измерений будет бесконечно возрастать по мере уменьшения единицы измерения и увеличения масштаба карты. Этот удивительный факт известен под названием «эффект Ричардсона».

Приближенные вычисления длины береговой линии острова Мальорка, выполненные с различной точностью. Измерения слева производились отрезком большей длины, чем на иллюстрации справа. Нетрудно видеть, что точность измерения на рисунке справа выше. Удивительно, но в соответствии с эффектом Ричардсона с ростом точности пределом измерений будет не истинная длина береговой линии, а бесконечность.

В свое время научное сообщество проигнорировало исследования Ричардсона, однако сегодня они считаются крайне важными, так как дали толчок к изучению фракталов. Бенуа Мандельброт цитирует Ричардсона в известной статье 1967 г. под названием «Какова длина побережья Великобритании?». В этой статье Мандельброт объясняет, что понятие длины для объектов неправильной формы, например для побережья, не имеет смысла. Как следствие, математики определили число, которое являлось бы количественной оценкой площади подобных объектов неправильной формы. Это число — экстраполяция числа «привычных» измерений объектов классической геометрии (одно, два, три измерения и так далее). Следовательно, «неевклидовы» объекты неправильной формы подобного типа часто имеют дробное число измерений.

Все зависит от способа измерения

Геометрия Евклида, в которой число измерений может быть только целым, не отражает всей сути фигур неправильной формы. Эксперимент Ричардсона равносилен вычислению длины в разных масштабах. Если мы измерим длину побережья из космоса, то полученный результат будет меньше, чем если мы, подобно муравью, пройдем вдоль всего побережья, считая каждую песчинку.

Рассмотрим в качестве примера клубок ниток. Издалека он кажется точкой, иными словами, фигурой с нулем измерений. Если наблюдатель подойдет ближе, то увидит, что клубок напоминает сферу, то есть имеет три измерения. Если он еще приблизится, то увидит, что в клубок свернута одна нить; таким образом, клубок будет иметь всего одно измерение. Когда наблюдатель приблизится настолько, что сможет рассмотреть структуру нити, то клубок снова станет трехмерным, поскольку станут видны отдельные волокна, из которых состоит нить. Подобный процесс можно продолжать и далее. Таким образом, очевидно, что о числе измерений клубка ниток нельзя говорить объективно: все зависит от положения наблюдателя, то есть от масштаба наблюдений.

Продемонстрируем эффект Ричардсона, сравнив приближенное значение длины окружности с одной стороны и периметр острова Мальорка — с другой. Пусть окружность имеет диаметр 100 км — это величина одного порядка с диаметром острова. Длина окружности будет в 71 раз больше диаметра, то есть 314,15… км. Поместим результаты на логарифмическую шкалу, чтобы лучше оценить результаты для разных растворов циркуля, которые мы будем применять при измерениях. Отметим на горизонтальной оси логарифм величины, обратной раствору циркуля, что можно интерпретировать как точность измерений: при малом растворе циркуля s точность измерений 1/s будет выше. На вертикальной оси будем отмечать логарифмы от рассчитанных значений периметра.

Для раствора циркуля, эквивалентного 50 км, наилучшим приближением окружности будет шестиугольник со стороной в 50 км и периметром в 300 км. Если в качестве приближения окружности мы выберем 12-угольник со стороной 25,882 км, то приближенное значение ее длины составит 310,584 км, для 24-угольника со стороной 13,053 км — 313,272 км, для 48-угольника со стороной 6,54 км — 313,92 км, для 96-угольника со стороной 3,272 км — 314,112 км и для 192-угольника со стороной 1,636 км снова получим длину, равную 314,112 км. Мы видим, что по мере уменьшения раствора циркуля приближенное значение длины окружности все ближе и ближе к реальному.

Однако при измерении длины побережья Мальорки все иначе. Если в качестве приближения выберем многоугольник со стороной 28 км, получим периметр 362,2 км, для многоугольника со стороной 14 км периметр будет равен 416,7 км, при стороне, равной 7 км, периметр будет равен 467,7 км, при стороне 3,5 км периметр достигнет 524,8 км.

В обоих случаях точки графика с хорошей точностью аппроксимирует прямая. Очевидно, нельзя ожидать, что точки будут лежать точно на одной прямой — это невозможно в силу неизбежной погрешности измерений. В случае с окружностью прямая расположена практически горизонтально; для береговой линии Мальорки прямая имеет наклон (угловой коэффициент d = 0,17). Уравнение прямой можно выразить в виде log l = d∙log (1/s) + k, где l — приближенное значение периметра для раствора циркуля s; d — рассчитанный угловой коэффициент прямой; k — некая постоянная. При переходе к экспоненциальной форме получим:

l = с/s^d,

где с — основание логарифма в степени k.

Заметьте, насколько эта формула похожа на закон Корчака.

Итог работы Ричардсона таков: традиционное понятие длины при измерении береговой линии не имеет смысла. Он предложил использовать новую величину, которую можно назвать «морщинистость», определяемую значением углового коэффициента d из предыдущего примера. Для реальных границ и побережий были получены следующие значения d:

d = 0,25 для западного побережья Британии, одного из самых изрезанных заливами берегов на планете;

d = 0,15 для границы Германии;

d = 0,14 для границы Испании с Португалией;

d = 0,13 для побережья Австралии;

d = 0,02 для южноафриканского побережья, одного из наиболее ровных берегов.

Фрактальные объекты в природе обычно можно увидеть в границах и деревьях.

К границам относятся границы между любыми двумя средами в биологии, физике, химии и так далее, а также между двумя разными поверхностями: границы между странами, берега рек, морские побережья, облака и многое другое.

К деревьям в этом смысле можно отнести все случаи ветвления с самоподобием: деревья, кусты и растения, бассейны рек, молнии и так далее.

Некоторые растения и бассейны некоторых рек при наблюдении с высоты имеют фрактальную структуру.

О покрытиях

Кривые, поверхности и объемные тела могут быть столь сложны, что измерение их параметров может вызвать серьезные затруднения. Однако длина, площадь и объем не изменяются произвольно в зависимости от выбранного масштаба, и существуют законы, позволяющие вычислить одну из этих величин, если известна другая. Закон, открытый Ричардсоном (а также открытия Корчака, Ципфа и Херста), согласно которому длина является степенной функцией точности с показателем степени d, будет полезен в обсуждении нового понятия — размерности.

В начале XX в. одной из крупнейших задач математики было определение размерности и ее свойств. Ситуация осложнилась, когда начали появляться различные виды размерности: топологическая, размерность Хаусдорфа, фрактальная, самоподобия и многие другие. Все они связаны между собой, в определенных ситуациях некоторые из них имеют смысл, а другие нет, иногда они совпадают, иногда отличаются. Вопреки тому, что можно было бы ожидать, не следует думать, будто существует некое единственное определение размерности, которое полностью раскрывает смысл этого понятия. Поиски единого приемлемого универсального определения, подобно поискам Святого Грааля, оказались безрезультатны.

Джеральд А. Эдгар в своей книге Measure, Topology and Fractal Geometry («Измерения, топология и фрактальная геометрия») так иллюстрирует понятие размерности:

«Пусть дана точка в трехмерном пространстве. Мы можем заключить ее внутрь куба, словно в тюрьму. Куб образован шестью плоскими гранями. Следует учитывать, что эти грани являются двумерными. Мы можем заключить точку на одной из этих граней в „тюрьму“, нарисовав вокруг нее небольшую окружность. Если грани куба являются двумерными, то нужно понимать, что окружность является одномерной. Точка, которая находится внутри одной из окружностей, может быть заключена в „тюрьму“ с помощью двух точек, которые будут стенами „тюрьмы“. Следует учитывать, что множество, содержащее всего две точки, имеет нулевую размерность. Наконец, точка, которая находится на множестве из двух точек, уже не может двигаться. Чтобы заключить ее в „тюрьму“, не нужно стен. По определению, это множество имеет размерность 0».

Идея определения размерности по индукции восходит к «Началам» Евклида, где неявно приводится похожая формулировка: говорят, что фигура является одномерной, если ее граница состоит из точек; двумерной, если ее граница образована кривыми; трехмерной, если ее граница состоит из поверхностей.

Пуанкаре заново рассмотрел этот вопрос, оперируя похожими терминами, и ввел понятие топологической размерности. Он дал такое определение: пространство имеет размерность n, если его можно каким-либо способом разделить пространством, имеющим размерность n — 1. Однако, чтобы это определение стало более строгим, нужно корректно определить значение формулировки «каким-либо способом разделить». В 1913 г. первую попытку уточнить это определение предпринял Брауэр, затем десять лет спустя Урысон. Каждый привел различные толкования, но для локально связных пространств они совпадают. Так, в настоящее время наиболее важными считаются три определения топологической размерности: индуктивное определение Урысона (и Менгера), индуктивное определение Брауэра (и Чеха), а также размерность Лебега, определенная посредством покрытий^[16].

Топологическую размерность Лебега (далее мы будем именовать ее просто топологической размерностью) очень удобно использовать для множеств, имеющих неправильную структуру.

Наглядно изобразить топологическую размерность очень просто. Покрытием подмножества S на ⁿ является семейство открытых множеств^[17] таких, что их объединение содержит множество S. На рисунке показано покрытие кривой на ².

Покрытие кривой с кратностью 2.

_{(Источник иллюстраций на этой странице: Мария Изабель Бинимелис.)}

Аналогичные действия можно выполнить для любой части заданной плоскости. Приведем простую аналогию. Пусть нужно закрасить определенную область зеленым цветом. У нас есть одна или несколько печатей, которые могут иметь круглую или другую форму. Покрытием этой области будет раскрашивание ее в зеленый цвет без промежутков. Очевидно, что некоторые участки будут покрыты несколько раз, поэтому они будут окрашены в более темный цвет. Выберем из всех таких участков один (или несколько) самого темного цвета, то есть такой, который был закрашен наибольшее число раз, и назовем это число кратностью покрытия. Взгляните на рисунок ниже.

Рассмотрим первое покрытие (слева) и обратим внимание на маленький участок, почти точку, закрашенный черным цветом: он покрыт пятью печатями, и нет никакого другого участка, который был бы покрыт большее число раз. Следовательно, кратность этого покрытия равна пяти. Можно ли уменьшить эту кратность? Иными словами, можно ли поставить печать на всех точках поверхности, не покрывая какую-либо точку пять раз? На рисунке справа видно, что это возможно: мы слегка уменьшили площадь печатей (каждая из них содержится внутри соответствующей печати, расположенной в том же месте на рисунке слева), и вся нужная область оказалась покрытой полностью. Это новое покрытие называется подпокрытием предыдущего. Для нового покрытия кратность уменьшилась до четырех.

Можно получить покрытие кратности 3, как показано на следующем рисунке, но покрытие кратности 2 уже невозможно.

Заданная область, каждый участок которой покрыт не более чем тремя печатями.

_{(Источник: Мария Изабель Бинимелис.)}

В целом говорят, что множество имеет топологическую размерность п, если наименьшая возможная кратность его покрытия равна n + 1. Следовательно, говорят, что топологическая размерность первой фигуры (кривой) равна 1, размерность второй фигуры (области) равна 2. Точка является 0-мерной, линия — одномерной, плоскость — двумерной, а евклидово пространство ⁿ является n-мерным.

С этой точки зрения размерность произвольного пространства (точки, линии, поверхности и других) соответствует минимальному числу параметров, необходимых, чтобы описать различные точки этого пространства. Например, чтобы описать все точки плоскости, достаточно всего двух координат: абсциссы (которая, например, определяет длину) и ординаты (определяет ширину). Пространство требует наличия уже трех координат: длины, ширины и высоты.

Необходимость ввести определение топологической размерности была в значительной степени вызвана тем, что традиционное определение размерности (в котором фигурировали интуитивно понятные и неточные термины, например «тонкость») было поставлено под сомнение в последние годы XIX в. Первое определение следует из доказательства Кантора, которое подтверждает взаимно однозначное соответствие между множеством точек вещественной прямой ¹ и вещественной плоскости ².Второе определение основано на том, что существует непрерывная функция ¹ на ², открытая Пеано.

О кривых, покрывающих плоскость

Одна из задач вычислений — это выполнение различных измерений, например, измерение длин кривых, площадей фигур, объемов тел и так далее. Иногда точно измерить длину кривой непросто, но можно получить приближенный результат с очень хорошей точностью, используя спрямление кривой (приближение кривой ломаными линиями или полигональное приближение). Чем меньше отрезки ломаной линии, тем точнее результат. На следующем рисунке показано приближение синусоидальной кривой отрезками ломаной линии, расположенными так, что концы отрезков лежат на этой кривой.

Приближение кривой ломаными.

Кривая называется спрямляемой, если длины вписанных в нее ломаных стремятся к определенному общему значению L, когда длины отрезков ломаных стремятся к нулю, то есть отрезки становятся все короче и короче. Это общее значение L и будет длиной заданной кривой. Для вычисления площадей используются аналогичные рассуждения с той лишь разницей, что вместо длин отрезков вычисляется площадь прямоугольников.

В приведенном примере мы используем различные объекты, имеющие топологическую размерность 1 (отрезки), чтобы вычислить приближенное значение объекта такой же размерности (кривой). Алгоритм действий удивительно остроумен и в то же время интуитивно понятен.

Существует ли вероятность аппроксимации объектов любой евклидовой размерности с помощью других объектов меньшей размерности? Например, можно ли найти приближенное значение площади квадрата с помощью кривой? Интуитивно понятно, что это невозможно: кривые не имеют толщины, следовательно, не могут покрывать пространство полностью. Иными словами, объект, имеющий топологическую размерность 1 (кривую) нельзя преобразовать в объект размерности 2 (например, в квадрат). Кажется, что предполагать обратное было бы попросту нелепо.

Кривая Пеано

Итальянский математик Джузеппе Пеано в 1890 г. открыл непрерывную кривую, проходящую через все точки квадрата с единичной стороной, то есть кривую размерности 1, которую можно преобразовать в объект размерности 2. Пеано следовал тем же путем, что и Кантор, который ранее доказал противоречащее интуиции утверждение: мощность бесконечного множества точек отрезка единичной длины равна мощности бесконечного множества точек любой поверхности, например квадрата с единичной стороной. Подробнее мы рассмотрим это революционное открытие несколько позже^[18].

Интуиция подсказывает, что непрерывная кривая — это «путь, которым следует точка при непрерывном движении». Чтобы устранить неоднозначность определения и подчеркнуть значимость открытия Пеано, Жордан в 1887 г. ввел следующее строгое определение непрерывной кривой: «Непрерывная кривая является непрерывным отображением отрезка, определенным для всех точек единичного отрезка». Стандартный алгоритм построения кривой Пеано — это повторяющийся процесс, при котором каждый из девяти отрезков исходной кривой заменяется кривой, сгенерированной на каждой итерации алгоритма.

Девять отрезков исходной кривой приведены на рисунке ниже (первый отрезок обозначен цифрой 1 и так далее):

Затем процесс повторяется для каждого из девяти исходных отрезков (иными словами, каждый из девяти отрезков заменяется всем рисунком) и так далее. В результате получим кривую следующего вида (на нижней тройке изображений углы срезаны, чтобы наглядно показать, что кривую Пеано можно построить, не отрывая карандаша от бумаги).

После бесконечного числа итераций кривая Пеано примет форму квадрата.

Однако сам Пеано нашел лишь аналитическое построение, но не определил этот итеративный процесс и также не смог изобразить эту кривую графически (однако он привел рисунок в виде перевернутой восьмерки, чтобы показать непрерывность найденной им кривой). Пеано просто показал, как именно график найденной им функции будет постепенно заполнять квадрат. Другие математики в попытках графически представить абстрактную функцию, описанную Пеано, предложили итеративный алгоритм ее построения, показанный на рисунках выше, а также на следующем рисунке:

Как следствие, мы не знаем, какую именно из этих кривых можно назвать собственно кривой Пеано. Обе они в пределе образуют одну и ту же фигуру — квадрат.

В статье Пеано, которая была опубликована в 1890 г., впервые описывалась кривая, покрывающая плоскость.

Также существуют варианты кривой Пеано, которые не покрывают плоскость. Одну из них можно получить аналогичным преобразованием исходных девяти отрезков с тем отличием, что вертикальные линии будут короче горизонтальных.

Еще одну кривую подобного вида можно получить, если удалить центральный отрезок. Эта кривая обладает интересным свойством: ее график является непрерывным, но функция, которая определяет эту кривую, непрерывной не является.

МУЗЫКА И МАТЕМАТИКА

Идея о том, что одномерный объект может целиком покрывать плоскость, легла в основу музыкальных композиций. Например, скрипач Скоп Джон сочинил 11-минутную композицию для контрабаса и английского рожка, в первой части которой два инструмента целиком заполняют ритмическое и тональное пространство. Когда начинает появляться новая тональность, один из двух инструментов немедленно переходит в другую тональность. В результате образуется своеобразное противостояние между длинными выразительными и быстрыми энергичными фразами. Во второй части оба исполнителя выдерживают единообразие формы и стиля. Неясные тональности первой части становятся более четкими. Если мы рассмотрим партитуру в различных масштабах, то заметим обилие схожих частей.

Кривая Гильберта

Еще до того, как появились графические изображения кривой Пеано, Давид Гильберт открыл другую кривую, которая также покрывает плоскость. Базовый принцип, лежащий в основе кривой Гильберта, слегка отличается от принципа кривой Пеано: используется не единственный шаблон, а несколько, и к каждому из них применяются различные правила. Подобные построения называются нестандартными.

Блестящий немецкий математик Давид Гильберт.

На рисунке показано, как на каждом шаге части кривой соединяются тремя отрезками, которые непрерывно уменьшаются в размерах. Именно так описал построение этой кривой сам Гильберт в 1891 г. в короткой статье всего на двух страницах. Существует стандартное построение этой же кривой, в основе которого лежит несколько иная фигура. Оставим поиски этого построения заинтересованному читателю. Отличие кривой Гильберта от кривой Пеано в том, что в первой на каждом шаге построения длины отрезков и квадратов уменьшаются в два раза, а в кривой Пеано — в три раза.

Существуют интересные вариации кривой Гильберта: в одной из них в качестве исходной фигуры используется перевернутая буква V, в другой, за авторством Карла Хансена, исходной фигурой является буква Н (очевидно, по первой букве фамилии Гильберта — Hilbert). Кривая Гильберта обладает еще одной любопытной особенностью: ее можно видоизменить так, что она будет покрывать объемную фигуру, как показано на рисунке:

Эта трехмерная версия кривой Гильберта имеет большое значение в устройствах передачи данных, в особенности там, где для выявления ошибок используется так называемый код Грея — вариация двоичного кода. В традиционном двоичном коде числа от 0 до 7 записываются так: 000, 001, 010, 011, 100, 101, 110, 111. Затем каждое число этой последовательности располагается в одной из вершин куба так, чтобы двоичные разряды соответствовали координатам этой вершины. Например, число 001 нужно расположить в точке с координатами (0, 0, 1). После этого числа нужно упорядочить, следуя вдоль кривой Гильберта, как показано на рисунке ниже.

Эта последовательность двоичных чисел является кодом Грея, который обладает особым свойством. При внимательном рассмотрении заметно, что соседние значения различаются только в одном разряде (одним битом информации), что не выполняется для традиционной последовательности чисел, где, например, за 001 следует 010 (эти числа отличаются двумя разрядами). Говоря техническим языком, расстояние Хэмминга между двумя соседними 3-битными числами равно 1. Если нам нужно закодировать не первые восемь натуральных чисел, а больше, то понадобится следующая итерация кривой Гильберта, с помощью которой мы закодируем числа от 0 до 31. Код Грея позволяет существенно снизить количество ошибок при передаче информации. В частности, он широко применяется в наземных сетях цифрового телевидения.

Кривая Гильберта также используется при цифровой обработке изображений. Если мы хотим распечатать изображение в градациях серого на лазерном принтере первого поколения, то нам понадобится приближенная бинарная модель изображения, так как принтер «понимает» только значение 0 или 1 (тонер/нет тонера). Для этого применяется так называемый дизеринг. Эта техника имитирует широкую палитру цветов, хотя в действительности используется крайне ограниченное число оттенков. Она также применяется при моделировании множества оттенков серого в двоичном коде.

На рисунке слева — исходное изображение в 256 оттенках серого (именно эта конкретная фотография обычно приводится в качестве примера в научных статьях, посвященных обработке изображений). На втором рисунке слева — увеличенное изображение с примененным эффектом дизеринга, который позволяет имитировать 256 оттенков серого, когда реальное число градаций серого меньше 256. Далее приведено еще два увеличенных изображения. Для генерации последнего использовалась кривая Гильберта.

Как правило, этот процесс обычно выглядит так: для преобразования изображения в 256 градаций серого используется проход по линиям или блокам пикселей. Каждому пикселю присваивается оттенок серого из сокращенной палитры цветов в зависимости от оттенков соседних пикселей таким образом, чтобы снизить общую ошибку. Как видно на втором рисунке, после применения дизеринга на изображении возникают характерные мелкие дефекты. Чтобы избавиться от них, вместо прохода вдоль горизонтальных линий используется обход вдоль кривой Гильберта, проходящей через все пиксели изображения. Преимущество этого метода заключается в том, что в этом случае отсутствуют ярко выраженные дефекты, которые нетрудно заметить при других способах обхода изображения.

Треугольники, губки и снежинки: фрактальная размерность

После публикаций Пеано и Гильберта многие другие математики стали предлагать похожие примеры. Среди них были Хельге фон Кох, Поль Леви и Эрнесто Чезаро, Вацлав Серпинский и Исаак Шёнберг. Швейцарский математик Хельге фон Кох в 1904 г. опубликовал статью «Об одной непрерывной кривой, не имеющей касательных, построенной с помощью методов элементарной геометрии». Под этим пугающим названием скрывалось нечто очень простое и столь же удивительное. Рассмотрим отрезок горизонтальной прямой, имеющий единичную длину. Заменим исходный отрезок четырьмя отрезками длиной 1/3 и получим первую кривую для итеративного построения, которое показано на рисунке ниже:

Если построить три копии кривой Коха на сторонах равностороннего треугольника, получится так называемая снежинка Коха. Эта кривая обладает удивительным свойством: ее длина бесконечна, а площадь закрашенной области — нет.

Мы уже определили понятие размерности для любых объектов и увидели, что существуют кривые, подобные кривым Гильберта и Пеано, которые имеют размерность 1, но покрывают область размерностью 2. Возникает необходимость дать понятию размерности другое определение, которое согласовывалось бы с результатами наших наблюдений. Кривая Коха будет идеальным примером, который проиллюстрирует наши рассуждения. Новая размерность, о которой мы поговорим далее, называется фрактальной размерностью. Затем мы продемонстрируем фрактальную размерность для фигур, не обладающих свойством самоподобия.

Понятие самоподобия более подробно обсуждается в следующей главе. Здесь же мы укажем лишь его некоторые основные свойства. Объект обладает самоподобием, если имеет ту же форму, что и его части. Части самоподобного объекта могут быть получены путем преобразований этого объекта, которые называются преобразованиями подобия. Например, если мы возьмем кривую Коха, уменьшим ее в три раза и сделаем три копии новой, уменьшенной кривой, то сможем соединить их так, что получитсяновая кривая Коха. Мы последовательно расположим копии кривой так, что первая будет располагаться горизонтально, вторая — с поворотом на 60°, третья — с поворотом на —60°, четвертая — вновь горизонтально.

Этим свойством обладают и другие, даже самые простые объекты: например, можно уменьшить отрезок в два раза, соединить между собой две его уменьшенные копии и снова получить исходный отрезок. Нечто подобное можно сделать с квадратом: его можно уменьшить в четыре раза, затем соединить четыре уменьшенные копии и снова получить исходный квадрат. Во всех структурах, обладающих свойством самоподобия, существует взаимосвязь между коэффициентом уменьшения r (коэффициентом масштаба) и количеством частей n, на которые делится исходный объект. Рассмотрим эту взаимосвязь подробнее.

В случае отрезка коэффициент уменьшения r = 1/2, а для восстановления исходного отрезка нужно n = 2 копии. Если коэффициент уменьшения r равен 1/3, то нам понадобится n = 3 копии. Следовательно, во всех случаях n = 1/r. В случае квадрата для коэффициента уменьшения r = 1/2 потребуется n = 4 копии, чтобы восстановить исходный квадрат. Если коэффициент уменьшения r равен 1/3, то нам понадобится n = 9 копий. Во всех случаях будет выполняться соотношение n = 1/г².

Выполнив аналогичные подсчеты для куба, получим, что при коэффициенте уменьшения, равном 1/2, для восстановления исходного квадрата потребуется 8 копий, при коэффициенте уменьшения, равном 1/3, — 27 копий. В обоих случаях справедливо соотношение n = 1/r³. Показатель степени г всегда совпадает с топологической размерностью исходной фигуры.

Однако если мы проведем подобные вычисления для кривой Коха, то получим, что в первой итерации n = 4, r = 1/3. В этом случае взаимосвязь уже не столь очевидна. Руководствуясь результатами, полученными для отрезка и квадрата, предположим, что аналогичное соотношение выполняется и для кривой Коха, следовательно, 4 = 3^D, где D — условная размерность рассматриваемой кривой. Вычислить D очень просто: нужно взять логарифм от обеих частей уравнения. Получим: log 4 = D∙log 3, D = log 4/log 3 = 1,2629. Если мы выполним аналогичные вычисления для второй итерации кривой, получим 16 = 9^D или, что аналогично,

Фотографии Нила, Амазонки и Великих озер, сделанные с самолета. Можно увидеть крайне неравномерную структуру, которая описывается с помощью моделей фрактальной геометрии.

Силуэт большой рыбы, которая съедает маленькую, — аттрактор системы из 11 итерируемых функций. Шесть из них описывают тело рыбы, четыре — хвост, еще одна — силуэт маленькой рыбы. На рисунке приведена третья итерация.

Скульптура, автора которой вдохновил тетраэдр Серпинского. Он строится аналогично треугольнику Серпинского, единственная разница состоит в том, что вместо трех треугольников на плоскости используются четыре тетраэдра в пространстве.

Построение кривой Такаги, или бланманже, из многоугольников. Каждый следующий многоугольник строится на основе предыдущего по алгоритму, известному как «смещение средней точки».

Его использовал еще Архимед для вычисления площади сегмента, ограниченного дугой параболы и ее хордой.

Для создания этих искусственных пейзажей использовался тот же алгоритм, что и при построении графика функции Такаги, но уже в трех измерениях, с некоторыми изменениями и со случайным набором параметров. Генерирование фрактальных пейзажей применяется при съемках многих фильмов.

Некоторые объекты природы, например облака, легче моделируются с помощью фрактальной, а не евклидовой геометрии. Симуляция облаков производится с помощью приема компьютерной графики, который называется плазма. В нем используется коэффициент рассеивания, от которого будет зависеть итоговый результат.

Генетический код растений и других живых существ строится по принципу наименьшего действия. Инструкции, определяющие рост живых организмов, записываются в генетическом коде максимально экономичным образом. Именно поэтому большинство из них обладает свойствами самоподобия и имеет фрактальную структуру.

Изображение объемного множества Мандельброта, полученное с помощью алгоритма, основанного на кривых потенциала. Высота точки определяется числом итераций, после которых орбита этой точки удаляется от начала координат.

Увеличенное изображение объемного множества Мандельброта вблизи вершины большой кардиоиды. Все множество Мандельброта в таком масштабе по размерам будет сопоставимо с орбитой Юпитера. Оно подобно необозримой вселенной, полной замысловатых узоров, в которой обитают слоны, морские коньки, улитки.

Слева направо и сверху вниз представлена последовательность увеличенных изображений множества Мандельброта. Центр каждого изображения примерно совпадает с центром предыдущего.

Множество Мандельброта и множества Жюлиа, соответствующие различным значениям с, использованным при их построении.

Графическое изображение аттрактора Лоренца. Представлена орбита точки в пространстве, движение которой описывают определенные дифференциальные уравнения. Эти уравнения моделируют поведение потока жидкости и других схожих процессов. Точка вращается вокруг двух центров, перескакивая с одной орбиты на другую бесконечное множество раз. По словам Джеймса Глейка, это великолепное изображение, подобное рисунку оперения совы или крыльев бабочки, стало символом первых исследователей хаоса.

D = log 4²/log З² = (2log 4)/(2log 3) = 1,2629. Для любой итерации это соотношение будет выполняться при D = 1,2629. Это число называется размерностью подобия и обозначается D_S, в отличие от других фрактальных размерностей. Оно вычисляется по следующей формуле:

D_S = log n / log (1/r).

Мы нашли взаимосвязь между коэффициентом уменьшения r (коэффициентом масштаба) и количеством частей n, на которые делится исходный объект.

Чтобы лучше понять определение размерности подобия, рассмотрим несколько классических математических объектов, обладающих свойством самоподобия. Первым из таких объектов, который был открыт задолго до кривой Пеано (она также обладает свойством самоподобия; ее размерность мы вычислим позднее), было канторово множество. В наши дни Георг Кантор известен прежде всего благодаря своим трудам о бесконечности, в которых, в частности, доказал, что между точками пространства ¹ и точками пространства ² существует взаимно однозначное соответствие (об этом мы упомянули выше). Канторово множество было описано в 1883 г. За необычный внешний вид его также называют канторовой пылью. Построить его достаточно просто: начнем с единичного отрезка и удалим его среднюю треть, то есть интервал от 1/3 до 2/3. Затем удалим из каждого из двух полученных отрезков его среднюю треть (длиной 1/9), затем удалим среднюю треть (длиной 1/27) у всех четырех полученных отрезков и так далее. Результатом построения и будет канторово множество:

Это множество сложно изобразить, так как оно постепенно «исчезает», но нетрудно представить, как оно будет выглядеть, если мы продолжим процесс построения. Заметим, что если мы уменьшим канторово множество в три раза, то получим его левую часть. Если мы сделаем копию полученного множества и перенесем ее на 2/3 вправо, то получим правую часть канторова множества. Таким образом, канторово множество состоит из двух частей, каждая из которых в три раза меньше целого. По формуле размерности подобия получим:

D_s = log 2 / log 3 ~ 0,6309.

В канторовом множестве отсутствует какая-либо связь между точками, следовательно, его топологическая размерность равна нулю. Как можно видеть, его размерность подобия больше, чем топологическая размерность.

Для кривой Пеано, которая строится из девяти отрезков, n = 9, коэффициент уменьшения равен 1/3. Следовательно, ее размерность подобия равна

D_s = log3 ²/ log 3 = 2.

Двумерным аналогом канторова множества является так называемый ковер Серпинского. Его впервые описал польский математик Вацлав Серпинский в 1916 г. Первые четыре итерации построения ковра Серпинского выглядят так:

Можно сказать, что при построении ковра Серпинского на каждой итерации мы удаляем центральный квадрат полученной фигуры. Ковер Серпинского можно построить и другим способом: для этого нужно удалить центральный отрезок при построении кривой Пеано из девяти отрезков. Так как его можно получить из восьми копий оригинала, уменьшенных в три раза, то его размерность подобия будет равняться log 8/log 3–1,8928. Серпинский показал, что полученная кривая является универсальной, то есть содержит любую кривую, которую можно построить на плоскости. Если мы выполним аналогичное построение, взяв за основу пятиугольник или любой другой правильный многоугольник, то получим бесконечное множество «ковров». Наиболее известный из них, который строится на основе треугольника, — это так называемый треугольник Серпинского, изучением которого также занимался этот польский математик. Этот треугольник тоже можно получить итеративным построением на основе кривой; он имеет топологическую размерность 1 и размерность подобия, равную log 3 / log 2 ~ 1,5850.

Первые итерации построения треугольника Серпинского

Если мы перейдем к трем измерениям и обобщим построение канторова множества для куба, получим еще один удивительный объект — губку Менгера, названную в честь австрийского математика Карла Менгера, который открыл эту фигуру в 1926 г., когда занимался изучением топологической размерности. Это также универсальная кривая, но уже в трехмерном пространстве. Она имеет размерность подобия, равную log 20/log 3 ~ 2,7268, так как ее можно получить из 20 кубиков, каждый из которых в три раза меньше всей фигуры.

Скульптурное изображение губки Менгера.

«Близким родственником» этой кривой является тетраэдр Серпинского, который строится путем удаления центрального из пяти одинаковых тетраэдров. Он имеет чуть меньшую размерность подобия, нежели губка Менгера: log 4 / log 2 = 2.

Тетраэдр Серпинского.

Теперь, когда мы знаем, как вычисляется размерность подобия, попробуем связать ее с показателем степени, который фигурирует в законе Ричардсона, описывающем измерение границ и береговых линий. Представим, что мы хотим найти формулу Ричардсона для берега воображаемого острова, который имеет форму снежинки Коха. Этот остров (назовем его остров Коха) образован тремя одинаковыми кривыми, каждая из которых состоит из четырех самоподобных частей; коэффициент уменьшения равен 1/3. Следовательно, будет разумным выбрать для измерения длины берега раствор циркуля, равный 1/3, 1/9, 1/27 и так далее. Измерим один из трех берегов острова. Начнем с раствора циркуля, равного 1/3. Допустим, что длина стороны исходного треугольника равна единице. Первое приближенное значение длины берега будет равно 4/3. Выбрав раствор циркуля, равный 1/9, получим значение длины 16/9. Выполнив аналогичные расчеты, получим, что для раствора циркуля s = 1/3^k имеем l = (4/3)^k.

Представим полученные значения на логарифмической шкале. Мы можем выбрать любое основание логарифма. Будем использовать логарифмы по основанию 3 — это упростит вычисления, так как коэффициент уменьшения равен 1/3. Вспомним, что уравнение прямой, найденное Ричардсоном, имеет вид log₃ l = d∙log₃ (1/s). Если мы подставим в нее значения, вычисленные для стороны острова, получим log₃ (4/3)^k = d∙log₃3^h. Упростив, получим d = log₃ (4/3) = 0,2619.

Вспомним, что размерность подобия для снежинки Коха равнялась D_s = 1,2629. Как видим, дробные части этих чисел совпадают. Можно показать, что для объекта, обладающего самоподобием, наклон прямой Ричардсона d и размерность подобия связаны следующей простой формулой: D_s = 1 + d. Это означает, что размерность подобия можно вычислить двумя способами. Первый основан на геометрических свойствах фигуры, в нем фигурирует число частей структуры, подобных всей структуре в целом, и коэффициент уменьшения. Этот способ мы уже неоднократно использовали. Второй способ заключается в измерении расстояний с помощью циркуля.

Заметим, что размерность, вычисленная по алгоритму Ричардсона, является обобщением размерности подобия (они отличаются на единицу). Иными словами, мы можем вычислить фрактальную размерность для кривых, которые не обладают свойством самоподобия, например для берегов или границ. Но как можно вычислить размерность объектов, которые напоминают по форме пятно, губку или облако? В этих случаях циркуль нам не поможет. Расчет фрактальной размерности объекта может оказаться трудной задачей. Существует множество фракталов, размерность которых до сих пор не удалось рассчитать.

В этом случае нужно использовать размерность Минковского-Булигана. Она также известна как размерность Минковского, или грубая размерность. Она широко применяется в науке, так как ее можно очень просто рассчитать с помощью компьютера. Она также схожа с топологической размерностью и размерностью подобия.

Рассмотрим, почему это так. Проанализируем покрытие объекта, для которого мы хотим вычислить размерность. Если этот объект находится на плоскости, будем использовать для покрытия круги сравнительно малого радиуса. Если же объект находится в пространстве, будем использовать сферы. Это схоже с топологической размерностью Лебега, определенной посредством покрытий. Чтобы мы могли использовать общее обозначение для отрезков прямой, кругов на плоскости и сфер в пространстве, будем говорить о «шариках» радиуса эпсилон (ε). Будем обозначать N (ε) число шариков радиуса ε. Вычислим натуральный логарифм от этого числа и разделим его на log (1/ε), что, в свою очередь, отсылает к определению размерности подобия. Вспомним, что, применяя последнюю формулу к различным коэффициентам уменьшения, мы всегда получали один и тот же результат. Для объектов, которые не обладают свойством самоподобия (именно такие объекты мы сейчас рассматриваем), это не так. Определим размерность Минковского D_m как

D_M = lim_e->0 (log N(ε) / log (1/ε)).

Иными словами, размерность Минковского равна значению выражения log N (ε) / log (1/ε), когда ε стремится к 0.

ОПТИМАЛЬНЫЙ МАРШРУТ КОММИВОЯЖЕРА

В 1912 г. Серпинский незадолго до того, как открыл треугольник, названный в его честь, занимался изучением кривой, которая строилась по рекурсивному алгоритму и покрывала плоскость.

Сейчас эта кривая используется для решения задачи коммивояжера, в которой необходимо найти кратчайший маршрут, проходящий через определенные точки плоскости. Одна из возможных стратегий — обойти точки в той же последовательности, которую описывает кривая Серпинского. Для этого необходимо, во-первых, сформировать подобную кривую и нарисовать ее так, чтобы она покрывала все нужные точки маршрута. Если это не удалось, нужно использовать кривую Серпинского следующей итерации. Как только нам удалось построить кривую, которая проходит через все требуемые точки, искомый маршрут найден. Этот алгоритм применяется, например, при расчете маршрутов доставки почтовых посылок. Он также позволяет сократить общее расстояние, которое проходит перо плоттера при отрисовке карт.

* * *

Иными словами, размерность Минковского равна значению выражения log N (ε) / log (1/ε), когда ε стремится к 0.

Эта формула находит свое применение при подсчете клеток. Выполняются практически те же действия, что и при измерении расстояний на карте с помощью циркуля. Дана фигура, размерность которой мы хотим найти. Фигура помещается поверх сетки с шагом ε, который принимает значения 1 мм, 1 см и так далее в зависимости от размеров фигуры. Затем подсчитывается число квадратиков или клеток, которые покрывает фигура. Будем постепенно уменьшать значение и подсчитывать соответствующее число клеток для каждого. Затем, подобно алгоритму Ричардсона, построим график, осями которого будут логарифмические шкалы. На оси абсцисс будем обозначать логарифмы 1/ε, на оси ординат — логарифмы N(ε). Угловой коэффициент прямой, аппроксимирующей точки графика, будет равен D_M. Эта процедура применима к любым прямым, плоскостям и пространствам.

Подсчет клеток привлекает своей простотой, но размерности Минковского не хватает некоторых свойств, желательных с теоретической точки зрения. Немецкий математик Феликс Хаусдорф (1868–1942) из Боннского университета занимался теорией измерений и предложил новое определение размерности. Оно не применяется на практике, но имеет большое теоретическое значение и порой полезно для сравнения размерности некоторых разнородных множеств, которые имеют одинаковую размерность Минковского. В целом размерность Хаусдорфа меньше или равна размерности Минковского.

Кривая дракона

Рассмотрим подробнее последнюю и самую удивительную кривую — так называемую кривую дракона. Впервые она была исследована в 1960 г. тремя физиками NASA — Хайвеем, Бэнксом и Хартером. Она приобрела популярность несколько позднее, когда Мартин Гарднер рассказал о ней в своей колонке «Математические игры» в журнале Scientific American. Ввиду того что эту кривую очень просто построить и она обладает удивительными свойствами, ее изучением занялись исследователи из самых разных разделов математики.

Согласно Гарднеру, Хайвей построил эту кривую, сложив пополам полоску бумаги так, как показано на рисунке. Чтобы получить кривую дракона, нужно много раз сложить полоску бумаги в форме буквы «V», а затем развернуть ее так, чтобы все углы в местах сгиба были прямыми.

Первые итерации построения кривой дракона.

_{(Источник: Мария Изабель Бинимелис.)}

ДРАКОН ЛЕВИ

Согнуть лист бумаги можно двумя способами: «долиной» и «горкой». При построении кривой дракона лист бумаги всегда сгибается «долиной». Если мы будем сгибать лист обоими способами поочередно, то кривая заметно изменится. Существует 16 способов построения кривой дракона, но лишь пять из них можно назвать основными. Один из них известен под названием кривой Леви. Для построения этой кривой на первом шаге нам понадобится половина квадрата, разрезанного вдоль диагонали.

Размерность Хаусдорфа для кривой Леви равна 2. Это означает, что кривая Леви заполняет плоскость. Однако нетрудно видеть, что кривая покрывает не квадрат, подобно кривой Пеано или Гильберта, а область неправильной формы. Здесь обнаруживается еще одно удивительное свойство этой кривой: размерность ее периметра равняется примерно 1,934.

ФРАКТАЛЫ И МЕДИЦИНА

Лишь недавно в медицине и физиологии начали рассматриваться количественные вероятности хаотической динамики, а традиционные принципы начали ставиться под сомнение. Традиционно считалось, что многие заболевания возникают из-за стрессов, которые нарушают «порядок» в организме: реакция организма сбивается, а ритм работы органов отклоняется от нормального. Однако в последние годы было обнаружено, что ритм работы сердца и других органов может быть в высшей степени неравномерным у молодых и здоровых людей, а старение и заболевания сопровождаются упорядочением ритма.

Тело человека полно фрактальных структур — их можно увидеть в структуре нервной системы, кровеносных сосудов и так далее. Функции этих структур очевидно различаются, но тем не менее они имеют некоторые общие физиологические свойства. Фрактальные сгибы и ветвления позволяют в значительной мере повысить площадь впитывающей поверхности (например, поверхности кишечника), полезной площади кровеносных сосудов, желчных путей, бронхов, нервной системы. Отчасти благодаря избыточности и нерегулярности фрактальные структуры устойчивы к повреждениям. Например, сердце продолжает биться, даже если система, отвечающая за передачу электрических сердечных импульсов, серьезно повреждена. Если прислушаться к тому, как бьется сердце, то мы услышим четкий и равномерный ритм. В состоянии покоя хорошо заметно, что частота пульса неизменна. Однако более тщательный анализ показывает, что сердечный ритм здорового человека даже в состоянии покоя подвержен заметным колебаниям. Если мы изобразим на графике частоту сердечного ритма в течение дня, то результат покажется нам неравномерным и на первый взгляд полностью случайным. Напротив, если представить частоту сердечного ритма на различных временных шкалах, то обнаружится самоподобие.

На двух графиках на следующей странице сравниваются различные показатели работы сердца больного (в верхнем ряду) и здорового человека (в нижнем ряду). На графиках показателей работы сердца больного человека практически отсутствуют колебания. На правом графике сравнивается сердечный ритм в конкретный момент и после определенной временной задержки. Точки графика, отражающего состояние больного человека, расположены очень близко друг к другу. Напротив, показатели здорового человека на всех графиках демонстрируют определенные отклонения в широком диапазоне. Парадоксально, но именно сердце здорового человека демонстрирует хаотичное поведение.

Почему кровеносная и другие системы, которыми управляет нервная система, демонстрируют хаотическую динамику? Подобная динамика обладает рядом преимуществ. Хаотические системы способны работать в широком диапазоне условий, следовательно, обладают гибкостью и приспособляемостью. Подобная пластичность позволяет справляться с непредсказуемыми изменениями среды.

* * *

Американский писатель Майкл Крайтон использовал кривую дракона в своем романе «Парк Юрского периода». В начале каждой главы изображена соответствующая итерация кривой дракона с кратким комментарием одного из героев романа Яна Малькольма — математика и специалиста по теории хаоса. В книге рассказывается о клонировании динозавров на основе их ДНК, и кривая дракона служит метафорой этого сложного и нестабильного процесса.

Кривая дракона в заголовках глав «Парка Юрского периода».

Граница этой кривой имеет неправильную форму, но, что удивительно, идеально вписывается в границы других кривых дракона так, что ими можно целиком замостить плоскость. Согнуть лист бумаги можно двумя способами: «долиной» и «горкой». Если мы будем сгибать лист разными способами на каждой итерации, то вид кривой заметно изменится. Существует 16 способов построения кривой дракона, но лишь пять из них являются основными.

В 1958 г. Мандельброт начал работу в научно-исследовательском центре IBM, где занимался анализом шумов и электрических помех. Он обнаружил, что шумы подчиняются определенному образцу: группы колебаний повторялись при разном масштабе наблюдений. Повторяющиеся шаблоны совпадали не полностью, а были статистически подобными. Но несмотря на это, такие колебания все равно нельзя было описать известными методами математической статистики. Мандельброт начал подробнее исследовать это явление, стремясь обнаружить подобные шаблоны, которые нельзя описать методами математической статистики, в других системах. В попытках дать ответ на эти вопросы он разработал методы наблюдений, основанные на самоподобии, и с их помощью открыл фракталы. Мандельброт показал, что эти методы являются очень мощным инструментом для изучения случайных событий в столь различных сферах, как геостатика, экономика, физика и медицина.

В этой главе мы уже увидели, что задолго до Мандельброта изучением фракталов занимались некоторые известные математики. Мир, который описывает геометрия Евклида, ограничивается кубами, конусами и сферами и образован прямыми линиями, плоскими поверхностями и окружностями. Вейерштрасс, Кантор, Пуанкаре, Пеано, Гильберт, Кох, Серпинский и Хаусдорф смотрели дальше и видели неясные очертания другого, удивительного мира — мира текстур, ветвей и расщелин, из которых состояли многочисленные и сложные объекты.

Фигуры, открытые этими математиками, бросали вызов общепринятым определениям. Эти фигуры часто называли математическими монстрами, сравнивали с патологиями и болезнями. Тем не менее революционные работы этих ученых существенно продвинули вперед всю математику в целом.

Глава 3 О далматинцах и драконах. Линейные фракталы

Мать-природа не посещала уроков геометрии и не читала книг Евклида Александрийского. Ее геометрия полна зазубрин, но с собственной логикой, причем такой, которую легко понять.

Нассим Николас Талеб. Черный лебедь

И в шедеврах Эшера, и в других похожих картинах можно увидеть, что повторяемость и самоподобие порождают объекты, противоречащие здравому смыслу, и увлекают зрителя в головокружительную бездну. Мы расскажем, как на основе понятия самоподобия и принципа непрерывности, введенного Лейбницем, формировался фундамент нового раздела геометрии. Философы до сих пор не пришли к единому мнению относительно понятия непрерывности. В математике это понятие изменялось, уточнялось, ему давались различные определения, пока оно не оформилось в окончательном виде. Важность понятия непрерывности в развитии математики очевидна уже потому, что это понятие всегда было одним из самых изучаемых.

Обычно считается, что пространство и время непрерывны. Некоторые философы также утверждают, что непрерывными являются все процессы в природе. Отсюда и знаменитый афоризм Лейбница: Natura non facit saltus («Природа не делает скачков»). В привычном смысле «непрерывный» означает «непрестанный, происходящий без перерывов». В математике, где точность имеет первостепенное значение, путь к точному определению непрерывности был долог и тернист. Даже определение функции долгое время было связано с понятием непрерывности^[19].

В терминах современной математики выразить утверждение, похожее на изречение Лейбница, довольно сложно. В последние годы XVIII в. считалось, что для непрерывных функций бесконечно малое изменение аргумента ведет к бесконечно малому изменению значения функции. В XIX в. ученые отказались от понятия «бесконечно малое»^[20], и это определение было заменено другим, где использовалось более точное понятие предела.

Если мы скажем, например, что функция не делает скачков, на языке математики это будет недостаточно точно. В попытках дать более точное определение можно прийти к следующему: график непрерывной функции должен быть связным (то есть его нельзя разделить на два открытых множества, пересечение которых будет пустым множеством), однако, возможно, следует сказать, что он должен быть линейно связным^[21] (любые две его точки можно соединить дугой некой кривой).

В действительности понятия функции, непрерывности и дифференцируемости имеют точные определения, которые изучаются в старших классах средней школы. В настоящее время функция называется непрерывной в точке, если односторонние пределы функции в этой точке совпадают с ее значением в этой точке^[22]. Однако при изучении функций часто бывает недостаточно анализа одной лишь непрерывности и возникает необходимость в определении каких-то дополнительных свойств. Одним из таких свойств является равномерная непрерывность. Равномерная непрерывность означает, что небольшие изменения аргумента приводят к небольшим изменениям значения функции и, кроме того, величина этих изменений зависит от величины изменений аргумента, а не от самого значения х (отсюда и характеристика «равномерная»). Любая равномерно непрерывная функция является непрерывной, но не наоборот.

Рассмотрим в качестве примера функцию f(х) = 1/х на множестве вещественных чисел. Эта функция является непрерывной, но не является равномерно непрерывной, так как при значениях х, близких к 0, значения f(х) изменяются очень быстро. Существуют и другие дополнительные характеристики непрерывных функций, например абсолютная непрерывность — более строгое ограничение, чем равномерная непрерывность.

Хотя чешский математик Бернард Больцано (1781–1848) предвосхитил появление точного определения непрерывности, длительное время его работы игнорировались. Идея, которая легла в основу современного определения непрерывности (по сути, идентичная идеям Больцано), принадлежит французскому математику

Огюстену Луи Коши (1789–1857), который описал непрерывность функции, использовав понятие предела. Так, согласно Коши, функция f(х) непрерывна в точке а. если справедливо соотношение:

lim_x->a f(х) = f(а).

Производная функции в точке равна тангенсу угла наклона касательной к графику функции в этой точке. Это утверждение, важнейшее в дифференциальном исчислении, было сформулировано совместно Ньютоном и Лейбницем. Определение дифференцируемости интуитивно понятно: если в некоторой точке кривая не имеет единственной касательной, то функция, описывающая эту кривую, не дифференцируема в этой точке. В начале XIX в. большинство математиков полагали, что непрерывная функция имеет производную (иными словами, касательная к графику этой функции однозначно определена) почти во всех точках.

Однако в 1872 г. Карл Вейерштрасс выступил в Берлинской академии наук с докладом, который потряс все математическое сообщество: он показал, что существует непрерывная функция, не дифференцируемая ни в одной точке. Эта функция определяется как сумма синусоидальных функций и имеет два параметра, а и Ь:

Когда а принимает значения от 0 до 1, функция является непрерывной. Однако Вейерштрасс доказал, что эта функция не имеет производной ни в одной точке, если Ь — нечетное целое число и ab > 1 + 3π/2. Английский математик Готфри Харолд Харди несколько позднее доказал, что достаточно, чтобы выполнялись неравенства ab > 1 и b > 1.

График функции Вейерштрасса при а = 0,7 и b = 9.

В своей работе Вейерштрасс упоминает Римана, который, по-видимому, исследовал похожую функцию ранее, в 1861 г., но не опубликовал свои результаты. Функция Римана также представляет собой сумму синусоидальных функций, но не содержит параметров, а индекс n в ней используется иначе:

Построить график функции такого вида непросто. На следующей иллюстрации представлен график функции Римана и колебания курса акций некоего банка в течение года. Этот пример показывает, что подобная кривая может описывать реальные события.

Первая функция такого типа была открыта не Вейерштрассом, а уже упомянутым Больцано, который примерно в 1830 г. обнаружил непрерывную функцию, не имеющую производной практически ни в одной точке. Рукопись была утеряна, опубликовали ее лишь после Первой мировой войны, когда ее обнаружил другой чешский математик, М. Яцек в Австрийской национальной библиотеке в Вене. В этой рукописи Больцано доказывает, что найденная им функция недифференцируема во всех точках за исключением множества, мера которого равна нулю. Позднее он доказал, что эта функция недифференцируема во всех точках.

В отличие от не дифференцируемых функций, заданных аналитически, из прошлых примеров, функция Больцано определяется как предел последовательности полигональных функций В₁(х), В₂(х), В₃(х)…, первые две из которых представлены на следующих графиках.

_{Источник: Мария Изабель Бинимелис.}

Последователями Вейерштрасса было найдено множество других непрерывных не дифференцируемых функций. То, что сначала казалось необычным, в итоге оказалось вполне привычным. Более того, в настоящее время известно, что количество непрерывных функций, которые также являются дифференцируемыми, относительно невелико.

Пудинг и палатка

В 1903 г. японец Тейджи Такаги (1875–1960) привел пример непрерывной функции, не дифференцируемой ни в одной точке, которая была проще, чем функция Вейерштрасса. Аналитически она задается очень похожим образом. Главное отличие заключается в том, что ее основным элементом является график функции, имеющий форму палатки в виде перевернутой буквы «V», представленный на иллюстрации:

Функцию Такаги, равно как и функцию Больцано, можно представить в виде суммы ряда полигональных функций. Алгоритм, с помощью которого строятся эти функции, называется «смещение средней точки». Он использовался еще Архимедом для вычисления площади сегмента, ограниченного дугой параболы и ее хордой. На рисунке ниже представлены различные этапы построения графика. Каждому последующему этапу соответствует более тонкая линия.

На первом шаге строятся две копии исходного графика. Затем возьмем первую копию и сместим ее среднюю точку влево в точку с координатами (1/4; 1). Точки ее основания будут иметь координаты (0; 0) и (1/2; 1). Выполним аналогичные действия со второй копией. Ее средняя точка будет иметь координаты (3/4; 1), а крайние точки — (1/2; 1) и (1; 0). Полученный многоугольник станет отправной точкой для второго этапа построения. Аналогично выполняется третий этап, и так до бесконечности. В пределе получим кривую, под которой расположены все кривые, построенные на предыдущих итерациях.

Эта кривая также носит название кривой бланманже за схожесть с французским десертом бланманже — разновидностью пудинга.

Если выполнить это построение в трех измерениях и выбирать смещения случайным образом, то получим изображение, которое будет очень похоже на реальный пейзаж. Подобным способом, например, был создан инопланетный пейзаж в блокбастере «Звездный Путь II. Ярость Хана» (режиссер Николас Мейер, 1982), а также знаменитая Звезда Смерти в фильме «Звездные войны. Эпизод VI; Возвращение джедая» (автор сценария Джордж Лукас, 1983).

Дьявольская лестница

В статье 1884 г., озаглавленной «О свойствах совершенных множеств точек», Георг Кантор описал в высшей степени странную функцию, определенную на единичном квадрате. Эта функция является непрерывной и возрастающей, ее производная равна нулю почти во всех точках, график этой функции от нуля до единицы направлен вверх без «скачков». На этом участке длина кривой, определяемой этой функцией, равна 2. Кроме этого, график функции обладает свойством самоподобия: часть, ограниченную осью абсцисс, можно разделить на шесть равных частей, которые будут иметь ту же форму, что и весь график в целом. Коэффициент сжатия вдоль горизонтальной оси будет равен 1/3, вдоль вертикальной — 1/2. Благодаря этим загадочным свойствам и форме, напоминающей лестницу, график этой функции получил название дьявольской лестницы. Существуют и другие графики с этим названием, но функция, приведенная здесь, была описана раньше других и является наиболее типичной.

Дьявольская лестница строится по рекурсивной процедуре. В центральной трети единичного квадрата на высоте 1/2 нужно провести отрезок, параллельный оси абсцисс. Затем следует провести две диагонали, соединяющие концы этого отрезка с вершинами единичного квадрата, как показано на рисунке. На втором этапе нужно выполнить аналогичные действия над остальными третями графика. Повторяя эти действия до бесконечности, мы получим дьявольскую лестницу.

_{Первые итерации построения дьявольской лестницы.}

_{(Источник: Мария Изабель Бинимелис.)}

Дьявольская лестница — это не просто график некоторой функции с примеча тельными свойствами. Она описывает свойства многих физических систем.

ДЬЯВОЛЬСКИЕ ЛИНЗЫ

В отличие от обычных, или преломляющих, линз, дифракционные линзы фокусируют лучи благодаря явлению дифракции, которое возникает при взаимодействии света с физической структурой линзы в форме концентрических колец различной плотности и (или) светопроницаемости. Существует разновидность дифракционных линз, известных как дьявольские линзы, которые обладают повышенной глубиной резкости и меньшими хроматическими аберрациями. Несмотря на зловещее название, эти линзы не содержат чего-то колдовского или сверхъестественного, что подтверждают их создатели: «Эти линзы получили такое название благодаря особому профилю, который был разработан по образцу фрактальной структуры, известной в математике под названием „дьявольская лестница"».

Эти линзы являются мультифокальными, то есть имеют несколько очень близко расположенных точек фокуса. Интенсивность света в фокусах линзы описывается фрактальной структурой. Мультифокальность линзы означает, что фокусы, соответствующие различным длинам световых волн, накладываются друг на друга; тем самым создается более четкое изображение. Это же свойство позволяет повысить глубину резкости, то есть расширить область, в пределах которой обеспечивается четкость изображения.

На фотографиях представлены дифракционные линзы под микроскопом. Видно, что они образованы множеством неравномерно расположенных концентрических колец. В основе строения этих линз лежит фрактальная структура. Мультифокальные линзы подобного типа используются для коррекции зрения.

Они также могут быть имплантированы внутрь глаза при операциях по удалению катаракты.

Что общего у губок, пылинок и снежинок?

Простейшие преобразования объектов, которые можно выполнить на плоскости, называются преобразованиями подобия. Как следует из названия, они преобразуют один объект в другой, подобный первому, то есть изменяют не форму объекта, а лишь его положение, размер или ориентацию. К преобразованиям подобия относятся параллельный перенос, сжатие и растяжение, вращение и отражение.

Кривая Коха, о которой мы рассказали в прошлой главе, обладает свойством самоподобия, так как состоит из нескольких (четырех) частей, подобных всей кривой в целом. Чтобы получить первую часть кривой (расположенную слева), нужно всего.\ишь уменьшить всю кривую в три раза и совместить левый конец кривой с левым концом полученной уменьшенной копии.

Чтобы получить вторую часть, нужно опять-таки уменьшить всю кривую в три раза, повернуть ее на 60° относительно горизонтальной оси и совместить ее левый конец с правым концом первой части кривой. Здесь мы используем параллельный перенос, сжатие и поворот — все эти преобразования являются преобразованиями подобия.

Можно выполнить аналогичные действия и с треугольником Серпинского. Нам не понадобится использовать поворот, достаточно параллельного переноса и уменьшения в три раза. Это же справедливо и для канторова множества (называемого также канторовой пылью), ковра Серпинского, губки Менгера и кривой дракона.

Добавим к повороту и симметрии два новых преобразования: одно из них позволяет изменять ширину и высоту фигуры в разных пропорциях, другое — поворачивать оси координат на разные углы. Получим множество преобразований, которые называются аффинными преобразованиями плоскости. Первое из этих двух преобразований позволяет трансформировать квадрат в треугольник, а с помощью второго, которое называется сжатием, можно превратить квадрат в ромб. Фрактальные структуры, которые можно получить с помощью подобных преобразований, называются самоаффинными. К ним относится очень известный «папоротник Барнсли», открытый британским ученым Майклом Барнсли. Можно заметить, что для его построения требуется четыре аффинных преобразования, одно из которых заключается в сжатии по ширине до нуля (так формируется стебель), второе, примененное трижды, — комбинация сжатия и поворота (представлено на рисунке), с помощью которого получаются ветви.

Папоротник Барнсли и его различные аффинные преобразования.

Используя эти преобразования, можно построить множество различных фракталов, которые называются линейными фракталами или системами итерируемых функций (от английского IFS — Iterated Function Systems). Эти системы получаются путем применения ряда преобразований к некоему множеству. Согласно формулировке, введенной Барнсли в книге «Фракталы повсюду», система итерируемых функций — это система функций, задающих определенное преобразование, которое затем выполняется на протяжении множества итераций. Результатом применения этих преобразований является так называемый аттрактор. Другими словами, аттрактор системы итерируемых функций — это форма, к которой стремится фрактал, когда указанные преобразования повторяются достаточно большое число раз. Может показаться удивительным, но аттрактор не зависит от изначальновыбранной исходной фигуры, на которой строится фрактал. Все фракталы, о которых мы рассказали в этой книге, можно построить, используя это множество преобразований.

Попробуем использовать систему итерируемых функций, чтобы описать кривую дракона, о которой рассказано в предыдущей главе. Несмотря на внешнюю сложность этой кривой, для ее построения нужно всего два преобразования. Чтобы показать, что форма итоговой кривой не зависит от исходного множества, построим кривую дракона сначала на основе отрезка, а затем на основе некоторой фигуры.

В случае с отрезком будем для простоты считать его длину равной единице. Сначала уменьшим отрезок в 1/√2 раз и повернем его на 45° против часовой стрелки. Поместим левый конец отрезка в точку с координатами (0, 0). Затем снова уменьшим исходный отрезок в 1/√2 раз и повернем его на 135° снова против часовой стрелки, поместив правый конец полученного отрезка в точку с координатами (1,1).

Нетрудно заметить, что полученные отрезки соприкасаются концами в верхней точке. Это возможно благодаря тому, что мы подобрали коэффициент уменьшения так, что отрезки образуют половину квадрата, разрезанного по диагонали. Применив эти же преобразования к кривой, полученной на первой итерации, получим следующую итерацию кривой дракона и так далее. Заметьте, насколько быстро кривая, полученная на промежуточных итерациях, приближается по форме к итоговой кривой дракона.

Кривая дракона, построенная на основе отрезка.

_{(Источник: Мария Изабель Бинимелис.)}

Во втором случае выберем в качестве исходной фигуры изображение щенка далматинца, которых в итоге станет 101, а может быть, и больше. Построение кривой дракона в этом случае будет аналогично построению на основе отрезка.

Кривая дракона, построенная на основе изображения далматинца.

_{(Источник: Мария Изабель Бинимелис.)}

Коллаж для воссоздания любого изображения

Мы увидели, как с помощью систем итерируемых функций можно получить некоторые классические фракталы, и показали, как при последовательном выполнении аффинных преобразований формируется некий аттрактор. Тем не менее по-настоящему интересно то, что для любого изображения можно описать систему итерируемых функций, аттрактором которой будет данное изображение. Другими словами, мы решим обратную задачу фрактальной геометрии.

В этом смысле одним из важнейших открытий является теорема коллажа, которую сформулировал Барнсли в 1985 г. Допустим, дано некоторое множество L и соответствующая система итерируемых функций. Чтобы узнать, в какой степени эта система функций аппроксимирует L, построим отображение L для каждой функции и объединим их в одно общее изображение. Отличие между исходным и полученным изображением подскажет, как можно приближенно описать множество L с помощью данной системы функций.

Например, допустим, что дано изображение кленового листа и мы хотим описать его с помощью системы итерируемых функций. Так как в теореме коллажа не уточняется, какую систему нужно выбрать, лучше довериться интуиции и попытаться сформировать коллаж из различных копий исходного изображения листа. Чтобы упростить процесс, в нашем примере мы будем использовать только аффинные преобразования и ограничимся тремя функциями. На следующих изображениях показано преобразование каждой копии, выделенное прямоугольной рамкой. Представим, что преобразованные копии являются прозрачными, и расположим их поверх исходного изображения. На рисунке черным цветом выделены покрытые части исходного изображения. Части изображения, выделенные разными оттенками серого, по теореме коллажа указывают, насколько далек аттрактор системы итерируемых функций от искомого изображения.

Написание программ, которые способны решить эту задачу для произвольных изображений, и сегодня остается актуальной темой исследований и вызывает большой интерес ученых.

Глава 4 Скрытый порядок

Когда в 1980 году я сказал друзьям, что вместе с X. Хаббардом работаю над многочленами второй степени от комплексной переменной… меня спросили: «И ты надеешься найти что-то новоеР».

Адриен Дуади

Вы уже знаете, что такое размерность, самоподобие и непрерывность, и теперь мы готовы с головой окунуться в обширный мир фракталов и познакомиться поближе с самым знаменитым из них — множеством Мандельброта. Не стоит забывать, что на основе очень простых правил можно построить чрезвычайно сложные фигуры, как вы уже увидели из предыдущих глав этой книги. Этот принцип выполняется не только для фракталов, о которых мы уже рассказали и о которых поговорим и в этой главе. Ему также подчиняется великое множество явлений природы. Фрактальная геометрия предлагает аналогии и модели, которые, возможно, помогут нам в будущем найти некий универсальный закон Вселенной. Если этот закон существует, то в нем должна учитываться его извечная противоположность — хаос.

Действительно ли Мандельброт открыл множество Мандельброта?

Множество Мандельброта, также именуемое множеством М, обладает многими примечательными свойствами. Возможно, самое привлекательное и загадочное из них таково: это множество бесконечно сложно, но строится по очень простым правилам, понятным любому, кто умеет складывать и умножать. Однако стоит отметить, что при построении множества Мандельброта сложение и умножение придется выполнить несколько триллионов раз. Поэтому множество Мандельброта было открыто только с появлением современных компьютеров.

Как мы расскажем позднее, теоретические основы, благодаря которым открытие множества Мандельброта стало возможным, были сформированы в 20-е годы прошлого столетия усилиями французских математиков Гастона Жюлиа (1893–1978) и Пьера Фату (1878–1929). В 1918 г. Жюлиа опубликовал несколько статей о комплексных числах, где описал свойства определенных множеств, которые в то время нельзя было изобразить графически. Позднее эти множества получили название множеств Жюлиа.

В 1978 г. французский математик Адриен Дуади (1935–2006) и американец Джон Хамал Хаббард (р. 1945) с помощью специально созданной программы смогли получить первые изображения множеств Жюлиа — нечеткие и невысокого качества. Годом позже Мандельброт опубликовал собственные изображения, полученные в научно-исследовательском центре IBM. Первое изображение множества Мандельброта датируется 1981 г. Оно было получено совместными усилиями Роберта Брукса и Петера Мательски.

Дуади и Хаббард подробно изучили множество Мандельброта, доказав, что оно является связным и компактным и что его внутренняя часть состоит из счетного множества компонентов. Наконец, они же записали каноническую формулу множества Мандельброта — квадратичную комплексную функцию z² + с.

В свое время Мандельброт сказал, что крупнейшей проблемой для исследователей при изучении этого множества станет написание алгоритма его визуализации. В своей книге «Фрактальные объекты» он признает первенство работ Жюлиа и Фату, а также отмечает: «Я работал так, как ненавидят работать теоретики: я любовался незабываемыми картинами, используя компьютер как микроскоп, имея в своем распоряжении примитивные инструменты 1980 года».

КОМПЛЕКСНЫЕ ЧИСЛА НЕ ТАК СЛОЖНЫ, КАК МОЖЕТ ПОКАЗАТЬСЯ

Вещественные числа обозначают все точки, расположенные на числовой прямой, причем каждому числу соответствует точка и каждой точке соответствует число. Существуют правила сложения, вычитания, умножения и деления вещественных чисел. Так называемые комплексные числа определяются аналогичным образом стой лишь разницей, что им в соответствие ставятся точки, расположенные не на прямой, а на плоскости, которая называется комплексной плоскостью. Существует три способа определения комплексных чисел: в прямоугольной системе координат, в полярных координатах и в алгебраической форме. Комплексные числа обычно обозначаются буквой z. В прямоугольных координатах любому комплексному числу z сопоставлена точка с двумя координатами — вещественной и мнимой. Мнимые координаты откладываются на вертикальной оси, мнимая единица обозначается буквой i. Мнимое число i является квадратным корнем из -1. Именно поэтому комплексные числа долгое время назывались мнимыми. Они не так сложны, как может показаться, и благодаря им удалось упростить многие теории и формулировки. Для обозначения комплексных чисел на плоскости используется прямоугольная система координат, в которой по горизонтальной оси откладывается значение вещественной части, по вертикальной оси — значение мнимой части. Запишем одно и то же комплексное число через декартовы координаты, в алгебраическом виде и в полярных координатах:

z = (1/2, √3/2) = (1/2) + (√3/2i) = 1_60°

В этой формуле z — комплексное число, вещественная часть которого равна 1/2, мнимая — √3/2. Это равносильно тому, что радиус-вектор соответствующей точки комплексной плоскости имеет длину 1 и образует угол в 60° с горизонтальной осью. Для сложения двух комплексных чисел достаточно сложить по отдельности их вещественные и мнимые части. Например, если z₁ = (-2,4) и z₂ = (3,1), их сумма равна (1, 5). Если представить эти числа графически, то мы увидим, что их сумма — это всего лишь точка на диагонали параллелограмма, образованного радиус-векторами этих чисел. Чтобы выполнить умножение, достаточно следовать простым правилам: i² заменяется на -1, так как i равно квадратному корню из -1:

z₁z₂ = (-2 + 4i)(3 + i) = —2(3 + i) + 4i(3 + i) = (-6 — 2i) + (12i — 4) = -10 + 10i.

Полученной точке соответствует радиус-вектор, угол которого равен сумме углов радиус-векторов данных чисел, а длина (которая называется модулем) равна произведению длин этих радиус-векторов.

Импульсивно-компульсивные вычисления

Важнейший вывод всех упомянутых работ был таков: с помощью очень простой формулы можно получить сложные результаты. Как мы увидим чуть позже, этот вывод имел большое значение для всей науки в целом.

В итеративной процедуре результат вычислений, полученный на предыдущем этапе, является входным значением для вычислений на следующем этапе. Суть этого метода в том, что с некоторым числом выполняется определенная операция, она же выполняется над полученным результатом, затем над результатом, полученным на следующем этапе, и так до бесконечности. В формальном виде это можно представить так:

x_n+1 = f(x_n).

Чтоб лучше понять, о чем идет речь, представим, что этой операцией является возведение числа в квадрат. В этом случае запись примет следующий вид:

x_n+1 = x_n²

Примем в качестве начального значения любое число, например x₀ = 2. Тогда на первом шаге получим х₁ = 2² = 4; затем х₂ = 4² = 16, х₃ = 16² = 256 и так далее. Полученная последовательность чисел (в нашем примере это последовательность 2, 4, 16, 256….) называется орбитой, а точка, к которой стремится эта последовательность (в нашем случае это бесконечно удаленная точка), называется аттрактором.

Если рассматривать эту же операцию возведения в квадрат, но выбрать начальное значение, меньшее 1, например x₀ = 0,5, то аттрактором будет 0. Если x₀ = 1, результат на любом шаге всегда будет равен 1. В этом случае говорят, что орбита состоит из одной точки, которая называется фиксированной точкой.

В конце XIX в. математики, физики и биологи проявляли большой интерес к итеративному процессу, в котором значение, полученное на предыдущем шаге, возводилось в квадрат и складывалось с некой константой. На языке математики это называется семейством квадратичных функций вещественной переменной. Интерес научного сообщества был вызван тем, что это семейство функций было связано с рядом различных теорий, которые со временем были объединены в так называемую теорию хаоса.

Точки-пленники, или Как найти выход из лабиринта

Жюлиа и Фату первыми исследовали итерируемые комплексные функции, и полученные ими результаты легли в основу всех последующих работ в области фрактальной геометрии. Помимо прочего, Жюлиа и Фату изучали поведение комплексных чисел при их последовательном возведении в квадрат и сложении результата с константой. В виде формулы это выражается так:

z_n+1 = z_n² + c,

где z — комплексное число, с — комплексная константа. Суть формулы проста: нужно взять число, умножить его на само себя, сложить с константой с и повторять эти действия над каждым полученным результатом снова и снова. В полученной последовательности комплексных чисел каждое число зависит только от выбора начальной точки и константы с.

В 1906 г. Фату доказал, что если применить эту операцию ко всем точкам комплексной плоскости, то большинство полученных орбит будут заканчиваться на бесконечности, за исключением четко определенного множества точек, внутренняя часть которого сегодня известна как множество Фату. Эти точки можно назвать «пленниками», а остальные точки — «изгнанниками». Точки на границе между ними, «охранники», образуют множество Жюлиа.

Рассмотрим подробнее эту операцию при с = (0, 0). Квадрат комплексного числа — это точка комплексной плоскости, модуль радиус-вектора которой равен квадрату модуля радиус-вектора исходной точки, а угол с горизонтальной осью в два раза больше исходного.

В следующей таблице приведены значения z, z², z⁴, z⁸, z¹⁶, z³² для трех разных комплексных чисел: внутри единичной окружности (иными словами, модуль этого числа меньше единицы), на единичной окружности и, наконец, вне единичной окружности. На рисунке приведено геометрическое представление всех трех случаев.

В таблице вверху приведены расчеты для трех типов орбит.

Орбита, описанная в левой части таблицы, стремится к началу координат; та, что в центре таблицы, описывает единичную окружность; та, что справа, уходит в бесконечность.

На рисунках представлено графическое изображение этих трех орбит на комплексной плоскости.

Мы видим, что для точки внутри окружности орбита стремится к началу координат, для точки вне окружности — уходит в бесконечность, а точка, которая находилась на единичной окружности, по-прежнему остается на ней. Чем больше модуль исходного числа, тем быстрее оно удаляется от единичной окружности. Таким образом, комплексная плоскость делится на две части: «пленников», которые находятся внутри единичной окружности, и точек вне ее, которым «удалось сбежать». В этом случае множество Жюлиа представляет собой единичную окружность — множество точек-«охранников». Заметим еще один факт (впоследствии он сыграет очень большую роль): множество Жюлиа инвариантно по отношению к квадратичной функции, то есть любая орбита, начало которой находится на множестве Жюлиа, останется на этом же множестве.

Заметим, что существуют две фиксированные точки: (0, 0) и (1, 0). В этом случае точка (0, 0) является аттрактором, так как к ней стремятся орбиты всех точек внутри окружности. Говорят, что в этом случае внутри единичной окружности располагается область притяжения аттрактора — точка (0, 0). Точка (1, 0) является неподвижной точкой — репеллером, так как рядом с ней существуют точки, например, (1, 01, 0), орбиты которых уходят в бесконечность.

Если мы будем считать бесконечность еще одной точкой плоскости и обозначим ее знаком <*>, то будем говорить, что точка °° является неподвижной, а ее область притяжения будет состоять из всех точек, лежащих вне единичной окружности.

Единичная окружность — простейший пример множества Жюлиа. Оно обладает теми же свойствами, что и большинство множеств Жюлиа: оно является границей области притяжения аттрактора (0, 0) и , динамика в окрестности точек этого множества неустойчива.

Частный случай z_n+1 = z_n², который обычно записывается в виде z —> z², — это своеобразный вход в мир удивительных и прекрасных фрактальных множеств Жюлиа.

Чтобы получить изображение других множеств Жюлиа, например для с = 0,5 + 0,5i, нам понадобится помощь компьютера. В теории для каждой точки плоскости нужно подтвердить, что ее орбита стремится к нулю или к бесконечности. На практике это невозможно, поэтому, чтобы изобразить множество Жюлиа, нужно использовать альтернативные алгоритмы.

На следующем рисунке показана таблица с данными для орбит нескольких точек, а также изображение множества Жюлиа, соответствующего с = 0,5 + 0,5i.

Три орбиты, которые уходят в бесконечность.

Орбиты для некоторых точек при с = 0,5 + 0,5i.

В верхней таблице орбиты всех точек уходят в бесконечность. В нижней таблице все орбиты стремятся к определенной неподвижной точке (-0,409, 0,275).

При рассмотрении таблиц можно увидеть, что если начальная точка очень удалена от центра, то есть модуль ее радиус-вектора очень велик, то орбита этой точки будет уходить в бесконечность. Но начиная с какого значения выполняется это правило? К счастью, на этот вопрос существует точный ответ. В общем случае радиус окружности будет наибольшим из двух чисел: 2 и модуля с. Любая орбита, начальная точка которой лежит вне этой окружности, будет уходить в бесконечность. Этот результат крайне важен для определения множества Мандельброта, что мы продемонстрируем несколько позже.

На основе этого факта можно разработать алгоритм, который позволит точно определить множество точек-«пленников». Первым приближением границы для с = 0,5 + 0,5i будет окружность радиуса 2. Если мы запрограммируем этот алгоритм так, что он будет обрабатывать пиксели экрана (каждой точке будет соответствовать пиксель), то получим очень большое множество точек (в зависимости от выбранной точности). Тем не менее это множество будет конечным. Компьютер вычислит значение выражения на первой итерации и пометит определенным цветом точки, которые уже на первой итерации оказались вне окружности радиуса 2. Остальные точки будут помечены черным цветом. Граница множества черных точек будет вторым приближением множества Жюлиа. Для оставшихся черных точек (на каждой итерации их будет все меньше) произведем вторую итерацию вычислений и выделим цветом точки, которые окажутся вне круга радиуса 2. Остальные точки по-прежнему будут черного цвета.

Эти действия будут повторяться для всех точек черного цвета, которых с каждым разом будет становиться все меньше, пока изменения множества черных точек не станут неразличимы на экране. Этот алгоритм, который называется алгоритмом времени убегания (escape time), для с = —1 дает следующее изображение множества Жюлиа:

Множество Жюлиа, соответствующее с = -1 с последовательными приближениями (изображены в виде линий вокруг множества точек черного цвета), рассчитанными по алгоритму времени убегания.

Различным значениям с соответствуют различные множества Жюлиа:

Анализ этих фигур показывает, что существует два принципиально разных класса множеств Жюлиа: те, которые образованы одной фигурой (такие множества Жюлиа называют связными), и те, что разделены на бесконечное множество отдельных точек вблизи друг от друга (такие множества называют несвязными).

На основании этой классификации можно разделить значения константы с, которую мы будем называть комплексным параметром, на два отдельных множества: те, которые порождают связные фигуры для итерации z_{n +1} = z² + с, и те, что порождают несвязные фигуры.

ИГРА В ХАОС

Алгоритм нахождения последовательных приближений множества Жюлиа работает очень медленно. Чтобы быстро получить достаточно детальное изображение множества Жюлиа, обычно используется другой алгоритм, который носит название игры в хаос. В предыдущей главе мы говорили о так называемых аффинных преобразованиях, которые при итеративном применении дают линейный фрактал. Теперь нам понадобится найти преобразования, которые при итеративном применении дают множество Жюлиа. Однако эти преобразования не могут быть аффинными, так как множества Жюлиа не обладают линейным самоподобием. В свою очередь, когда к точкам, находящимся вблизи множества Жюлиа (и вне его) применяются итеративные преобразования z —> z² + с, орбита этих точек уходит в бесконечность. Иными словами, множество Жюлиа выступает в роли репеллера. Если же теперь мы рассмотрим обратное преобразование, то множество Жюлиа будет уже не репеллером, а аттрактором. Как записывается это обратное преобразование? Пусть w — следующая точка итерации w = z² + с. Если мы хотим перейти к предыдущей операции, нужно выделить z из этого уравнения. Получим два решения:

z = +√(w — c);

z = -√(w — c).

Игра в хаос выглядит так: выбирается произвольная начальная точка, затем рассчитываются два изображения в соответствии с предыдущими преобразованиями. Процесс повторяется для всех полученных точек, результаты отображаются на экране. Чем больше итераций мы выполним, тем точнее будет полученное изображение множества Жюлиа.

Вселенная в одной песчинке

Деление множеств Жюлиа на связные и несвязные возникло не случайно. Именно в ходе исследований множества Жюлиа был открыт один из самых удивительных математических объектов — множество Мандельброта.

На первый взгляд, составление подобной классификации множеств Жюлиа невозможно, так как считалось, что для этого нужно проанализировать все возможные точки всех возможных множеств Жюлиа для каждого параметра с, которых бесконечно много. Однако Мандельброт использовал теорему, которую независимо друг от друга доказали Жюлиа и Фату примерно в 1919 г. Согласно этой теореме, орбита точки 0 определяет, является ли множество Жюлиа связным или нет. В частности, эта теорема подтверждает, что если орбита этой точки уходит в бесконечность, то множество Жюлиа несвязное; в противном случае множество Жюлиа является связным. Эта теорема имеет огромное значение, так как теперь достаточно выполнить итерацию для единственной точки z₀ = (0,0), чтобы определить природу множества Жюлиа.

Это очень точный и удобный способ выяснить, является ли множество Жюлиа связным. Но когда можно считать, что орбита точки (0, 0) уходит в бесконечность? Это нам уже известно: орбита уходит в бесконечность, если в какой-то момент она выходит за пределы окружности радиуса 2 и радиуса, равного |с|.

Мандельброт использовал это свойство, чтобы определить значения константы с, для которой множества Жюлиа являются связными. Когда он изобразил полученный набор значений с на комплексной плоскости, то увидел удивительную фигуру.

Грубо говоря, множество Мандельброта можно считать кардиоидой (кривой в форме сердца), которой касается бесконечное множество окружностей, среди которых выделяется одна наибольшего размера, расположенная слева от кардиоиды. При увеличении этой окружности становится видно, как она соединяется нитями с другими «аналогичными» структурами. Хотя кажется, что повсюду разбросаны отдельные точки, никак не соединенные друг с другом, в действительности множество Мандельброта является связным.

Множество внутренних точек этого множества имеет размерность 2. Несмотря на то что топологическая размерность границы множества Мандельброта равна единице, в 1991 г. японский математик Мицухиро Шишикура доказал, к удивлению многих, что ее размерность Хаусдорфа равна двум^[23].

Если внимательно изучить последовательность кругов все меньшего диаметра, которые расположены вдоль горизонтальной оси, можно заметить следующее правило: отношение диаметров соседних кругов стремится к константе, примерно равной 4,6692… Это значение, которое называется постоянной Фейгенбаума, фигурирует в описании множества природных явлений. Причины этого до сих пор неясны.

Изображения множества Мандельброта будут более красивыми, а его границы — более отчетливыми, если использовать алгоритм времени убегания и палитру из нескольких разных цветов. Будем выделять разными цветами точки с различной скоростью убегания. Например, будем обозначать точку зеленым цветом, если ее орбита выходит за пределы окружности радиуса 2 за 11–20 итераций, желтым — если требуется 21–30 итераций (смотрите цветную вкладку в конце книги).

Множество Мандельброта во всем своем великолепии.

Область, расположенная между большой окружностью и кардиоидой, получила название «долина морского конька». В ней обитает множество фигур, которые соединены тысячами разных способов и по форме напоминают морского конька. По всей плоскости располагаются уменьшенные копии целого множества, связанные между собой нитями разной формы. Множество Мандельброта, по-видимому, является фракталом в том смысле, в котором мы ранее использовали это понятие, то есть обладает свойством самоподобия в различном масштабе наблюдений. Однако в действительности это не совсем так. При каждом увеличении мы видим все больше нитей, поэтому всегда можем определить степень увеличения изображения. Существуют серьезные сомнения относительно самоподобия множества Мандельброта. Если нам показать два изображения множества Жюлиа, мы не сможем определить их масштаб, в то время как сделать это для множества Мандельброта несложно. Поэтому множество Мандельброта считается почти самоподобным.

На рубеже XX–XXI вв. китайский математик Тан Лэй выполнил ряд системных исследований множества Мандельброта и его динамики. Некоторые результаты представлены в его книге «Множество Мандельброта: Тема с вариациями» (2000). Изображение множества Мандельброта, приведенное на предыдущей странице, поможет понять всю важность фракталов за пределами математического мира.

Тема с вариациями

Как связано положение точки с в множестве Мандельброта и множество Жюлиа, при генерации которого использовалось это значение с? Это достоверно неизвестно. Можно заметить, что множество Мандельброта содержит всю информацию о форме всех множеств Жюлиа, уменьшенных и видоизмененных. Следовательно, оно является не просто средством классификации связных и несвязных множеств Жюлиа. Например, для всех значений с внутри кардиоиды множество Жюлиа будет напоминать деформированную окружность. Если точка, которой соответствует значение с, располагается внутри одной из касательных окружностей, множество Жюлиа будет разделено на доли. Если же эта точка располагается на одной из многочисленных нитей, то соответствующее множество Жюлиа будет разделено на несколько ветвей. В случае когда эта точка расположена на границе множества, соответствующее множество Жюлиа будет разделено на бесконечное число отдельных частей.

Изучив свойства множества Мандельброта более подробно, мы увидим, что внутри определенной касательной окружности число долей соответствующего множества Жюлиа всегда будет неизменным. Присвоив каждой доле соответствующее число и проанализировав полученные изображения, можно составить карту множества Мандельброта.

Множество Мандельброта и различные множества Жюлиа, рядом с которыми приведены соответствующие значения с, использованные при построении.

Создать целую вселенную, полную замысловатых узоров, цветов, улиток и драконов, можно не только с помощью последовательности квадратичных функций. Существует множество других итераций над комплексными числами, позволяющих создать особый фрактальный мир. Те примеры, с которыми вы успели ознакомиться, очень хорошо показывают, что сложная структура не обязательно строится по сложным правилам. Примеры этому можно найти и в природе. Достаточно вспомнить, что человечество во всем своем многообразии лиц имеет в своей основе один генетический код. Может случиться так, что все это окажется не просто совпадением. Когда-нибудь это поможет открыть универсальный закон Вселенной, о котором мы говорили в первой главе этой книги.

Звук хаоса^[24]

Во второй половине XX в. музыка и математика, искусство и наука снова начали сближаться благодаря использованию компьютерных программ для цифровой обработки данных. В конце 1910-х гг. Иосиф Шиллингер, советский музыковед, эмигрировавший в США, разработал систему музыкальной композиции, основанную на периодических колебаниях. Он увязал их с ритмом, тоном, гаммами, аккордами и аккордовыми последовательностями. Система изложена в семи книгах, в каждой из которых уделено внимание отдельному аспекту музыкальной композиции. Некоторые ученые считают, что Шиллингер описал создание музыки на компьютере задолго до появления первых компьютеров. По мнению некоторых экспертов, теория Шиллингера до сих пор не получила заслуженного признания, хотя очень серьезно повлияла на Джорджа Гершвина, Глена Миллера (оба были учениками Шиллингера) и Бенни Гудмена.

Модели, основанные на уравнениях и случайных последовательностях, чаще всего использовались при написании музыкальных композиций, но с 1970-х гг. стало возможным создавать алгоритмы на основе фракталов. По мнению многих, фрактальную музыку нельзя назвать подлинным искусством, так как искусство эмоционально, интуитивно и выразительно, в то время как наука рациональна, описательна и доказуема. Однако в большинстве подобных композиций фрактальная музыка служит лишь отправной точкой. Композитор создает фрактальную мелодию, которая сама по себе звучит странно и беспорядочно, затем изменяет ее, пока не получит приятную для слуха композицию. Этот процесс выполняется медленно, а результатом, по мнению многих авторов, будет чисто «компьютерная» музыка. Однако сам по себе компьютер никогда не смог бы создать похожее произведение.

Существует множество программ для создания фрактальной музыки (MusiNum, LMUSe, Gingerbread, The Well Tempered Fractal), которые позволяют автоматически генерировать приятные мелодии. Фил Томпсон, британский программист и музыкант-любитель, начал заниматься фрактальной музыкой как хобби и в 1998 г. выпустил первый альбом Organized Chaos. Его композиции, которые он сам считает открытиями, основаны на множестве Мандельброта. Томпсон создал программу Gingerbread, которая работает следующим образом. Выбирается начальная точка z, затем к ее орбите, получаемой с помощью квадратичной функции, применяются определенные преобразования, в результате чего координаты точек превращаются в ноты. Когда орбита выходит за границы окружности радиуса 2, мелодия начинается снова. Программа предлагает невероятное множество вариантов. Таким образом, с ее помощью можно создать огромное число разнообразных композиций. Без знаний математики и музыки можно создавать классические композиции и поп-музыку, начиная от саундтреков к фильмам и заканчивая фоновой музыкой для сайтов. Создатель программы гарантирует, что количество исходных данных бесконечно велико. Он определяет фрактальную музыку как особую форму композиции, при которой пользователь не «изобретает», а «открывает» музыку.

В поисках определения

Существует ли точное определение фрактала? Мандельброт в книге «Фрактальные объекты» утверждает, что существует только эмпирическое определение и что ни одно теоретическое определение не является полностью удовлетворительным. Иногда говорят, что фракталы — это объекты с дробной размерностью, но это утверждение вдвойне ошибочно, так как размерность фракталов может быть иррациональным (как, например, для треугольника Серпинского) или целым числом (для кривых, покрывающих плоскость, или для границы множества Мандельброта).

Возможно, точнее всего можно определить фрактал через его свойства: фрактал — это фигура, обладающая самоподобием (составные части подобны всей фигуре целиком), которая строится посредством итеративного процесса, зависит от начальных условий и имеет сложную структуру, несмотря на простоту алгоритма построения. Британский математик Кеннет Фальконер в своей книге Fractal Geometry. Mathematical Foundations and Applications («Фрактальная геометрия. Математические основы и приложения», 1990), определяет фрактальную структуру как структуру, обладающую одним из нижеперечисленных свойств:

1. Она слишком неравномерна, поэтому ее нельзя описать в терминах классической геометрии.

2. Ее детали заметны при любом масштабе наблюдений.

3. Она обладает самоподобием в некотором смысле (точным, примерным или статистическим).

4. Ее размерность Хаусдорфа-Безиковича строго больше ее топологической размерности.

5. Она строится с помощью простого рекурсивного алгоритма.

В 1975 г. Мандельброт дал фракталам такое определение: фракталы — это фигуры, которые являются результатом повторяющихся математических процессов, описываются не дифференцируемыми функциями, обладают самоподобием в любом масштабе и имеют фрактальную размерность.

Его не полностью устраивало это определение, и в 1982 г. Мандельброт определил фрактал как множество, у которого размерность Хаусдорфа строго больше, чем топологическая размерность. Тем не менее он сам признавал, что это определение недостаточно общее и не описывает отдельные объекты, которые являются фракталами, в частности кривые, покрывающие плоскость, к которым относятся кривая Пеано и кривая Гильберта (о них подробно рассказывается в первой части второй главы)^[25].

Можно принять точку зрения Барнсли, который понимал фракталы как аттракторы систем итерируемых функций, а можно придерживаться определения, которое приводит Джудит Седерберг в книге A Course in Modern Geometries («Курс современной геометрии», 2001). Оно звучит так: фрактал — это множество точек, обладающее самоподобием в строго детерминированном или строго стохастическом (случайном) смысле. Множество Мандельброта не удовлетворяет ни одному из этих определений, что может представлять некоторые неудобства (или наоборот). Седерберг пишет по этому поводу:

«Природа (или математическое описание?) множества Мандельброта — это наглядная аналогия того, что в музыке называется «тема с вариациями»: одни и те же шаблоны повторяются повсюду, но всякий раз несколько по-разному… Рассматривая его, мы постоянно будем видеть что-то новое, но при этом снова и снова будут появляться знакомые очертания. Благодаря этой неизменной новизне, множество Мандельброта можно назвать предельным фракталом, так как оно содержит другие фракталы внутри себя. По сравнению с обычными фракталами оно содержит больше элементов, обладает большей гармоничностью, а его неожиданные свойства еще более неожиданны».

САМООПРЕДЕЛЯЕМЫЕ ФРАКТАЛЫ

Существуют различные классификации фракталов по их свойствам. В зависимости от степени самоподобия все фракталы можно разделить на пять больших категорий:

1. Самоповторяющиеся. Эта категория накладывает наиболее строгие ограничения, так как необходимо, чтобы фрактал не изменялся в зависимости от масштаба наблюдений. К этой группе относятся канторово множество, треугольник Серпинского, кривая Пеано, снежинка Коха, кривая дракона, губка Менгера и так далее.

2. Линейные — те, которые строятся с помощью аффинных преобразований. Фракталы этого типа содержат уменьшенные копии всей фигуры целиком, но видоизмененные с помощью линейных функций, как, например, лист папоротника Барнсли.

3. Самоподобные. Фракталы этого типа содержат уменьшенные копии фигуры целиком, видоизмененные с помощью нелинейных функций, как, например, множество Жюлиа.

4. Квазисамоподобные. Фракталы этой группы более или менее идентичны в различном масштабе. Такие фракталы содержат уменьшенные и деформированные копии всей фигуры целиком. Как правило, к этому типу относятся фракталы, определенные с помощью рекурсивных процедур, как, например, множество Мандельброта или фрактал Ляпунова.

5. Статистически самоподобные. Эти фракталы обладают меньшим уровнем самоподобия. В них присутствует какая-либо числовая или статистическая метрика, которая не изменяется в зависимости от масштаба. Сюда относятся случайные фракталы, например траектория броуновского движения, полет Леви, фрактальные пейзажи и броуновские деревья.

Природа не фрактальна

В книгах, посвященных фракталам, часто можно встретить утверждения вида «в природе существует множество фрактальных объектов». В действительности это не совсем так. Когда мы говорим, что, например, граница, дерево или венозная сеть являются фракталами, в действительности имеется в виду, что для них существуют фрактальные модели достаточно высокой точности. В реальном мире не существует фракталов, как не существует прямых или окружностей.

Однако математические модели, описывающие реальность, помогают нам лучше понять ее. Подобно тому как теория относительности описывает орбиту Меркурия точнее, чем ньютоновская механика, фрактальная геометрия описывает форму некоторых объектов точнее, чем геометрия Евклида. Возможно, она точнее описывает и динамику реальных процессов.

Множество Мандельброта содержит бесконечно много деталей, и его рассмотрению в различных масштабах можно посвятить всю жизнь. Точно так же мы можем изучать и реальный мир, начав с молекул, затем перейдя к атомам, а от них — к нейтронам и другим субатомным частицам. Возможно ли, что в один прекрасный день мы достигнем предела? Или же, подобно множеству Мандельброта, предела не существует и здесь? Этого никто не знает.

Избавляемся от мечты о детерминизме

В словарях хаос определяется как «беспорядочная материя, неорганизованная стихия», существовавшая в мировом пространстве до образования известного человеку мира. Однако у ученых есть что добавить к этому определению.

Математическая теория хаоса является частью точной науки. В ней нет места неточностям и неопределенности. Разумеется, название теории хаоса восходит к традиционному смыслу этого слова, но хаос в математике — это не волк, а скорее овца в волчьей шкуре: он открывает нам дорогу в мир хаотичных структур и систем, которыми мы со временем научимся управлять.

Фрактальная геометрия и хаос тесно связаны друг с другом, и понять один из этих разделов математики без другого непросто. Фрактальная геометрия изучает самоподобные и парадоксальные фигуры, а теория хаоса изучает поведение непредсказуемых процессов и занимается поисками упорядоченности в них. Оба этих раздела математики, которые бурно развиваются в последние 20 лет, связаны между собой: среди хаоса формируются фракталы, которые можно использовать в попытках дать определение хаосу. Где же находится точка пересечения теории хаоса и фрактальной геометрии? Теория хаоса возникла в так называемой теории динамических систем. Любая динамическая система состоит из двух частей: состояния (обычно выражается через координаты) и динамики (изменения состояния с течением времени). Эволюцию динамической системы можно представить движением точек в координатном пространстве, каждой точке которого соответствует некое состояние системы. Это пространство называется фазовым пространством. Если эволюция системы подчиняется некоторому закону или законам (даже если их природа неизвестна), они неизменны с течением времени и последующее состояние можно описать через предыдущее, то речь идет о так называемой детерминированной динамической системе. Определение «детерминированная» означает, что эволюцию системы можно предсказать.

Один из самых удивительных результатов современной физики заключается в том, что предсказать поведение многих детерминированных динамических систем через длительные промежутки времени невозможно, так как на каждой итерации накапливаются ошибки. Подобные детерминированные динамические системы, которые очень чувствительны к относительно небольшим изменениям, называются хаотическими. Столь высокая чувствительность означает, что две возможные траектории перемещения точек, которые изначально расположены очень близко друг от друга, с течением времени могут очень сильно разойтись. То, что подобным поведением отличаются системы с большим количеством переменных, было известно давно. Однако, что удивительно, этой же особенностью обладают и очень простые системы.

В 1776 г. французский математик Пьер Симон Лаплас категорично заявил, что если бы ему были известны скорость и положение всех частиц во Вселенной в определенный момент времени, то он смог бы с идеальной точностью узнать прошлое и предсказать будущее. Свыше 100 лет это утверждение казалось верным. Из него следует, что свободы воли не существует, так как все детерминировано, по меньшей мере в теории. Такое видение мира позднее стало называться детерминизмом Лапласа. Применительно к науке оно означает, что если нам известны законы, которым подчиняется некое явление, известны начальные условия и даны средства расчетов, то мы можем с полной уверенностью предсказать будущее состояние изучаемой системы.

В конце XIX в. Пуанкаре задался вопросом, будет ли Солнечная система неизменно стабильной. Этот французский математик первым задумался над вероятностью того, что поведение системы существенно зависит от начальных условий:

«Поведение системы можно проанализировать, повторяя один и тот же эксперимент с одинаковыми начальными значениями в одинаковых условиях, чтобы было возможным получить одинаковые результаты. Это приводит нас к принципу причинности. Если одни и те же причины ведут к одним и тем же следствиям, речь идет о сильной причинности. Однако вбольшинстве случаев возможно достичь лишь схожих начальных условий, поэтому говорить о сильной причинности нельзя. Схожие причины имеют схожие следствия».

В 1903 г. Пуанкаре так охарактеризовал случайность: «Случайность служит мерой нашего невежества».

Наука XX в. засвидетельствовала крушение детерминизма Лапласа, вызванное двумя разными причинами. Первая вытекает из принципа неопределенности Гейзенберга в квантовой механике. Согласно ему существует фундаментальное ограничение точности, с которой можно измерить положение и скорость частицы. Однако непредсказуемость поведения системы в целом (и вторая причина, опровергающая детерминизм Лапласа) вызвана не принципом Гейзенберга.

В крупном масштабе некоторые события являются предсказуемыми, другие — нет. Траекторию полета мяча можно предсказать, траекторию полета воздушного шара, которая подчиняется дуновению ветра, предугадать не получится. И мяч, и воздушный шар подчиняются законам Ньютона. Но почему предсказать траекторию движения воздушного шара сложнее? Движение воды в тихой реке стабильно, равномерно, и его можно легко описать с помощью уравнений. Тем не менее в других условиях движение воды может быть нестабильным, непостоянным, могут образовываться завихрения. Чем обусловлена эта принципиальная разница? Советский физик Лев Ландау предположил, что с ростом скорости движения воды совокупность колебаний, по отдельности простых, приводит к тому, что поведение всего потока в целом предсказать нельзя. Однако было доказано, что теория Ландау ошибочна. Явления природы становятся непредсказуемыми из-за роста ошибок измерения и, как следствие, из-за неопределенности эволюции системы ввиду ее хаотической динамики. Именно хаотическая динамика и является второй причиной краха детерминизма Лапласа. Квантовая механика подтверждает, что начальные измерения не могут быть абсолютно точными, а хаотическая динамика делает невозможными любые попытки предсказать поведение системы.

Бабочка в Бразилии и моль в Сингапуре

Как мы уже отмечали, первым математиком, который «открыл» хаос или по меньшей мере попытался интуитивно понять его, был Пуанкаре. В 1890 г., когда Пуанкаре работал над решением астрономической задачи трех тел (суть задачи — определить положение и скорости трех тел произвольной массы, взаимодействующих по закону тяготения Ньютона, например Солнца, Земли и Луны, в любой момент времени), он обнаружил, что тела в этой задаче могут вращаться по хаотическим орбитам. Спустя восемь лет его соотечественник Жак Адамар опубликовал работу о хаотическом движении трех частиц, имевшую огромное влияние, в которой доказал, что траектории этих частиц нестабильны и отклоняются друг от друга. Адамар анализировал движение трех частиц при наличии трения вдоль поверхности с отрицательной кривизной. Эта поверхность впоследствии получила название «бильярд Адамара».

В 1963 г. американский математик и метеоролог Эдвард Лоренц занимался изучением определенных уравнений, которые, как он надеялся, помогли бы предсказывать погоду, и попытался представить их графически с помощью компьютеров. Самые быстрые компьютеры того времени были довольно медленными по сравнению с сегодняшними, поэтому как-то раз Лоренц вышел попить чаю, пока компьютер не закончит расчеты. Вернувшись, он обнаружил очень странную фигуру, которая получила название аттрактора Лоренца.

Графическое изображение аттрактора Лоренца.

Лоренц посчитал, что произошла какая-то ошибка, и повторил расчеты несколько раз, но результат не изменился. Тогда он подумал, что проблема заключена в самой системе. Тщательно изучив ее и подставив различные параметры, он заметил, что начальные условия были очень похожими, но результаты симуляций заметно отличались. Лоренц обратил внимание на то, что система, созданная им самим, позволяла указывать начальные условия с точностью не более трех знаков после запятой, но в действительности программа работала с шестью знаками после запятой, а три последних знака задавались случайным образом. Лоренц пришел к выводу, что эти незначительные, практически незаметные ошибки в начальных условиях увеличивались экспоненциально. К сожалению, Лоренц опубликовал свои результаты в специализированных метеорологических журналах, и о них никто не вспоминал почти десять лет.

Это явление, которое сегодня носит название чувствительности к начальным условиям, упоминается уже в работах Адамара и неявно в работах Пуанкаре. Если углубиться в историю, то можно вспомнить шотландского физика Джеймса Клерка Максвелла, который в 1876 г. занимался изучением различных хаотических событий, например искр, с которых начинается лесной пожар, или камня, с падением которого обрушивается лавина^[26].

Лоренц опубликовал свои открытия в 1963 г. в документе, предназначенном для Нью-Йоркской академии наук, в котором привел комментарий, оставленный его коллегой-метеорологом: «Если эта теория верна, то взмах крыльев чайки может навсегда изменить погоду». Позднее, согласно все тому же Лоренцу, когда он не мог подобрать название для речи, с которой должен был выступить на заседании Американской ассоциации содействия развитию науки в 1972 г., его коллега, Фелипе Мерилис, предложил такое название: «Может ли взмах крыльев бабочки в Бразилии вызвать торнадо в Техасе?».

В любом случае нет никаких сомнений, что Лоренцу был известен следующий отрывок из «Силы слов» Эдгара По:

«К примеру, когда мы жили на Земле, то двигали руками, и каждое движение сообщало вибрацию окружающей атмосфере. Эта вибрация беспредельно распространялась, пока не сообщала импульс каждой частице земного воздуха, в котором с той поры и навсегда нечто было определено единым движением руки. Этот факт был хорошо известен математикам нашей планеты. Они достигали особых эффектов при сообщении жидкости особых импульсов, что поддавалось точному исчислению — так что стало легко определить, за какой именно период импульс данной величины опояшет земной шар и окажет воздействие (вечное) на каждый атом окружающей атмосферы».

Суть открытия Лоренца, которое позднее получило название «эффект бабочки», такова: существует вероятность, что малейшее изменение начальных условий системы, подобное движению воздуха, вызванному взмахом крыла бабочки, по отношению к климату Земли может повлечь за собой цепочку последствий, которые окажут существенное влияние на всю систему^[27].

Хотя выражение «бабочка, которая машет крыльями» дошло до наших дней, о местонахождении бабочки и последствиях взмаха ее крыльев ведется обширная дискуссия, которую мы не будем воспроизводить в этой книге.

Притяжение хаоса

Если динамическая система будет функционировать достаточно долго, в ее фазовом пространстве появится множество точек, которое называется аттрактором. Аттрактором может быть точка, кривая, поверхность или какое-то сложное множество неправильной структуры, которое называют странным аттрактором.

Фрактальный характер хаоса проявляется в странных аттракторах. Если изобразить орбиты странного аттрактора и последовательно увеличивать их, то можно заметить самоподобие, характерное для фракталов.

Иногда динамические системы зависят от определенного параметра, благодаря чему их проще использовать при моделировании реальных систем. Значение этого параметра особенно важно, чтобы понять, как рождается хаос. При определенных значениях параметра динамическая система демонстрирует нормальное поведение, но иногда даже после малейших изменений появляется хаос. Особенно важную роль играет изучение этих систем и параметра, определяющего их поведение, с целью выявить точки перехода, в которых система начинает проявлять хаотические свойства.

Существование подобных динамических систем, в которых сосуществуют порядок и хаос, заставляет нас признать, что они тесно взаимосвязаны: в любой упорядоченной системе всегда явно или неявно присутствует хаос, а в любой хаотической системе явно или неявно присутствует порядок. Если система демонстрирует все более хаотическое поведение или, напротив, становится стабильной и упорядоченной, она потенциально может снова изменить свое поведение.

Примером того, как хаотическая система неявно является упорядоченной, может служить солитон Джона Рассела. Если мы бросим камень в пруд, на поверхности воды возникнут небольшие волны, которые вскоре исчезнут. Однако в 1834 г. шотландский ученый Джон Скотт Рассел (1808–1882) заметил крайне странное явление: в некоторых ситуациях волны порождали новую волну со своими характеристиками, и эта новая уединенная волна, так называемый солитон, могла проходить сотни километров, не теряя формы. Рассел несколько километров следовал за подобной волной вдоль канала и констатировал, что она шла против течения, не ослабевая. Солитон Рассела — это физическое явление, при котором сочетание дисперсии и нелинейности порождает упорядоченность.

На практике солитон Рассела используется для повышения качества передачи данных в оптоволоконных сетях. Так, в 1988 г. удалось передать солитон на расстояние свыше 4 ООО км.

Переход от ламинарного к турбулентному течению потока — один из наиболее наглядных примеров того, каким путем может рождаться хаос. В эксперименте Тэйлора-Куэтта поток проходит между двумя концентрическими цилиндрами, вращающимися с разной скоростью. С ростом скорости вращения внутреннего цилиндра поток перестает быть равномерным и разбивается на множество водоворотов. Еще более заметные изменения происходят, когда внешний и внутренний цилиндры вращаются в противоположных направлениях. В этом случае в потоке появляются спирали и завихрения. С изменением скорости вращения обоих цилиндров открывается своеобразный ящик Пандоры: в потоке появляются волнистые и турбулентные спирали. Результаты будут отличаться в зависимости от того, скорость какого цилиндра будет увеличена первой.

На фотографии изображен воссозданный солитон Джона Скотта Рассела в канале Юнион близ Эдинбурга. 12 июля 1995 г.

Фракталы и теория хаоса — относительно новые разделы математики, которые невозможно было бы исследовать без мощных современных компьютеров. Нет никаких сомнений, что «случайные» явления теперь описываются и классифицируются точнее, чем раньше. Однако удивительное, революционное открытие случайного поведения некоторых очень простых детерминированных систем приводит к очевидному парадоксу: хаос является детерминированным. Несмотря на то что четко заданные правила не содержат никакого элемента случайности, тем не менее они порождают случайные события.

Открытие вездесущности хаоса можно считать третьей революцией в физике XX в. наряду с появлением теории относительности и квантовой механики.

Библиография

BARNSLEY, М., Fractals Everywhere, San Diego, Academic Press, 1988. CEDERBERG, J.N., A Course in Modern Geometries, Nueva\ork, Springer, 2000. PEITGEN, H-O., Jurgens, H. у SAUPE, D., Chaos and Fractals, New Frontiers of Science, Nueva\ork, Springer-Verlag, 1992.

VV.AA., Las matematicas en la vida cotidiana, Madrid, Addison-Wesley, 1999. WAHL, B., Exploring Fractals on the Macintosh, Reading (Massachusetts), Addison-Wesley, 1995.

* * *

_{Научно-популярное издание}

_{Выходит в свет отдельными томами с 2014 года}

_{Мир математики}

_{Том 10}

_{Мария Изабель Бинимелис Басса}

_{Новый взгляд на мир. Фрактальная геометрия}

_РОССИЯ

_{Издатель, учредитель, редакция:}

_{ООО «Де Агостини», Россия Юридический адрес: Россия, 105066, г. Москва, ул. Александра Лукьянова, д. 3, стр. 1}

_{Письма читателей по данному адресу не принимаются.}

_{Генеральный директор: Николаос Скилакис}

_{Главный редактор: Анастасия Жаркова}

_{Старший редактор: Дарья Клинг}

_{Финансовый директор: Наталия Василенко}

_{Коммерческий директор: Александр Якутов}

_{Менеджер по маркетингу: Михаил Ткачук}

_{Менеджер по продукту: Яна Чухиль}

_{Для заказа пропущенных книг и по всем вопросам, касающимся информации о коллекции, заходите на сайт www.deagostini.ru, по остальным вопросам обращайтесь по телефону бесплатной горячей линии в России:}

_{® 8-800-200-02-01}

_{Телефон горячей линии для читателей Москвы:}

_{® 8-495-660-02-02}

_{Адрес для писем читателей:}

_{Россия, 170100, г. Тверь, Почтамт, а/я 245,}

_{«Де Агостини», «Мир математики»}

_{Пожалуйста, указывайте в письмах свои контактные данные для обратной связи (телефон или e-mail).}

_{Распространение:}

_{ООО «Бурда Дистрибьюшен Сервисиз»}

_{УКРАИНА}

_{Издатель и учредитель:}

_{ООО «Де Агостини Паблишинг»}

_{Украина Юридический адрес: 01032, Украина, г. Киев, ул. Саксаганского, 119}

_{Генеральный директор: Екатерина Клименко}

_{Для заказа пропущенных книг и по всем вопросам, касающимся информации о коллекции, заходите на сайт www.deagostini.ua, по остальным вопросам обращайтесь по телефону бесплатной горячей линии в Украине:}

_{® 0-800-500-8-40}

_{Адрес для писем читателей:}

_{Украина, 01033, г. Киев, а/я «Де Агостини»,}

_{«Мир математики»}

_{Украiна, 01033, м. Киiв, а/с «Де Агостiнi»}

_{БЕЛАРУСЬ}

_{Импортер и дистрибьютор в РБ:}

_{ООО «Росчерк», 220037, г. Минск, ул. Авангардная, 48а, литер 8/к, тел./факс: +375 17 331 94 27 Телефон «горячей линии» в РБ:}

_{® + 375 17 279-87-87 (пн-пт, 9.00–21.00)}

_{Адрес для писем читателей:}

_{Республика Беларусь, 220040, г. Минск, а/я 224, ООО «Росчерк», «Де Агостини», «Мир математики»}

_{КАЗАХСТАН}

_{Распространение:}

_{ТОО «КГП «Бурда-Алатау Пресс»}

_{Издатель оставляет за собой право увеличить рекомендуемую розничную цену книг. Издатель оставляет за собой право изменять последовательность заявленных тем томов издания и их содержание.}

_{Отпечатано в соответствии с предоставленными материалами в типографии:}

_{Grafica Veneta S.p.A Via Malcanton 2 35010 Trebaseleghe (PD) Italy Подписано в печать: 30.10.2013 Дата поступления в продажу на территории России: 25.03.2014}

_{Формат 70 х 100 / 16. Гарнитура «Academy». Печать офсетная. Бумага офсетная. Печ. л. 5.}

_{Усл. печ. л. 6,48.}

_{Тираж: 200 000 экз.}

_{© Albert Violant i Holz, 2010 (текст)}

_{© RBA Collecionables S.A., 2011 © ООО «Де Агостини», 2014}

_{ISBN 978-5-9774-0682-6 ISBN 978-5-9774-0623-9 (т. 10)} 

Примечания

1

В отличие от Гесиода, орфизм считает Хаос потомком Хроноса и Ананке.

(обратно)

2

Несмотря на это, руководствуясь современными критериями точности, Бертран Рассел указал, что четвертое определение из первой книги «Начал» является «бессмысленным», и возмутился тем, что это определение до сих пор включают в учебники.

(обратно)

3

В 1899 г. немецкий математик Давид Гильберт написал труд «Основания геометрии», в котором на основе 21 аксиомы (постулата) доказываются элементарные теоремы геометрии. Гильберт также исправил некоторые неточности в работе Евклида.

(обратно)

4

Согласно Проклу, понятия «общее утверждение» и «аксиома» являются синонимами для Аристотеля и других логиков, хотя в «Началах» никогда не говорится об аксиомах (axiómata), а Аристотель предпочитает вести речь о принципах (archai) и общих предпосылках (tá коná). По-видимому, постулаты и общие утверждения появились именно в геометрии, хотя последние общеупотребительны во всей математике. Общие утверждения выражают фундаментальные свойства математических объектов, а постулаты определяют возможные геометрические операции. Под постулатом будем понимать утверждение, которое очевидно считается истинным. Сегодня под аксиомами понимаются не очевидные истины, а логические выражения (предположительно верные), используемые в дедукции. Постулат стал архаичным синонимом аксиоме.

(обратно)

5

Евклид совершил еще одну ошибку, опустив как минимум два постулата. Первый из них гласит: две окружности, удаленные друг от друга на расстояние, меньшее двух их радиусов, пересекаются в двух точках. Второй звучит так: если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

(обратно)

6

Исходная формулировка этого постулата, эквивалентная данной, такова: «И если прямая, падающая на две прямые, образует внутренние и по одну сторону углы, меньшие двух прямых, то, продолженные неограниченно, эти прямые встретятся с той стороны, где углы меньше двух прямых».

(обратно)

7

Ошибочное доказательство, приписываемое Фалесу Милетскому, основано на предположении, что существует четырехугольник, все углы которого прямые. Однако существование прямоугольников нельзя доказать, не используя постулат о параллельности прямых.

(обратно)

8

Перспектива, от латинского perspicere — «проникать взором», эквивалентна греческому термину optiké — «оптика». Изначально перспективой называлось изучение зрительных феноменов. Именно в таком значении это понятие использовалось в Античном мире и в Средние века. То, что понимается под перспективой начиная с эпохи Возрождения и до наших дней, в Античности именовалось scaenographia. Эта дисциплина охватывала как изображения зданий, так и рисунки театральных декораций.

(обратно)

9

На языке математики проективным называется геометрическое преобразование, которое оставляет неизменным соотношение между отрезками гармонической четверки точек А, В, С и D так, что АВ/СВ = DA/DC.

(обратно)

10

В общем случае это алгебраические уравнения, в которых фигурируют производные. Подобные уравнения описывают поведение потоков, движение тел в силовых полях и многое другое.

(обратно)

11

Ферма доказал, что свет распространяется по тому пути, вдоль которого время движения минимально, а не вдоль пути, имеющего минимальную длину. Это еще раз доказывает, что физические законы зависят не от равенства углов, а от соотношения их синусов.

(обратно)

12

Чтобы множество, на котором определена некая операция, являлось группой, должны выполняться следующие условия. Операция должна обладать свойством ассоциативности; это означает, что для любых трех элементов множества а, b, с результат операции не зависит от того, в каком порядке группируются элементы. Далее, должен существовать нейтральный элемент; иными словами, множество должно содержать такой элемент е, что результатом операции над этим элементом и любым другим элементом а этого множества всегда будет элемент а.

Наконец, для каждого элемента должен существовать обратный. Это означает, что для любого элемента а этого множества должен существовать элемент a^-1 этого же множества, такой, что результатом операции над элементом а и обратным ему будет нейтральный элемент.

(обратно)

13

Николя Бурбаки — коллективный псевдоним группы французских математиков, которые в 1930-е гг. задались целью пересмотреть основы математики, используя крайне строгий подход. Среди членов группы были такие знаменитые математики, как Анри Картан, Жан Дьёдонне, Андре Вейль, Жан-Пьер Серр и Александр Гротендик.

(обратно)

14

Если использовать более точные математические термины, то не существует изометрического погружения (то есть такого, которое сохраняет расстояния) полной (то есть такой, где геодезические линии можно продлевать бесконечно) гиперболической плоскости в , хотя существуют локальные погружения, например псевдосфера, а также погружения, где первая производная является непрерывной.

(обратно)

15

В этой метрике расстояние между двумя точками Р и Q определяется как d(P,Q) = |ln(PA∙QB/PB∙QA)|, где А и В — точки на границе круга, через которые проходит единственная прямая, проходящая через Р и Q. (РВ — обычное евклидово расстояние между точками Р и В, аналогично для РА, QB и QA.) Это определение, автором которого является выдающийся британский математик Артур Кэли, подтверждает свойства этой метрики и точно выражает увеличение расстояния по мере приближения одной из точек к границе круга. Для точки, лежащей на границе круга, это расстояние будет бесконечно велико.

(обратно)

16

По определению Брауэра, размерность, равную —1, имеет пустое множество и только оно. Размерность пространства — наименьшее целое n такое, что для любого элемента этого пространства существует ряд произвольно малых открытых множеств с границами, размерность которых строго меньше n.

(обратно)

17

Чтобы определить открытое множество, сначала нужно понять, о каком пространстве идет речь и какая метрика используется. В нашем случае для простоты рассматривается реальное пространство с евклидовой метрикой.

(обратно)

18

Преобразование, открытое Кантором, взаимно однозначно, но не непрерывно. Пеано, напротив, ставил целью найти непрерывное преобразование единичного отрезка в квадрат с единичной стороной, которое не было бы взаимно однозначным (иными словами, несколько точек единичного отрезка отображались бы в одну и ту же точку). Это означало, что отрезок единичной длины и квадрат с единичной стороной не являются эквивалентными. Строгое доказательство этому нашел голландский математик Ян Брауэр в 1911 г.

(обратно)

19

Лобачевский в 1838 г. дал такое определение: «Функция от х есть число, которое дается для каждого х и вместе с х постепенно изменяется. Значение функции может быть дано или аналитическим выражением, или условием, которое подает средство испытывать все числа и выбирать одно из них, или, наконец, зависимость может существовать и оставаться неизвестной».

(обратно)

20

В современных теориях, например в нестандартном анализе, эти понятия снова стали использоваться, но уже в другой трактовке.

(обратно)

21

Любое линейно связное множество является связным, но не наоборот.

(обратно)

22

Это определение эквивалентно определению непрерывности Коши — Вейерштрасса или определению на языке эпсилон-дельта.

(обратно)

23

Размерность Хаусдорфа для множеств Жюлиа варьируется в зависимости от значения с. Для с = i размерность Хаусдорфа приблизительно равна 1,2; для с = —0,123 + 0,745i она равна примерно 1,3934. Все эти значения найдены эмпирическим путем, а точная размерность для большинства из них неизвестна.

(обратно)

24

В основу этого раздела легла книга Musica fractal: El sonido del caos («Фрактальная музыка: звучание хаоса») Хуана Антонио Переса Ортиса, члена кафедры языков и информационных систем университета Аликанте, Испания.

(обратно)

25

Топологическая размерность кривых, покрывающих плоскость, равна 2, так как именно такую размерность будет иметь фигура, полученная в финальной итерации.

(обратно)

26

Выражение «зависимость от начальных условий» стало широко использоваться еще в 1906 г. после публикации П. Данхема.

(обратно)

27

Возможные последствия невинного взмаха крыла бабочки изобразил Рэй Бредбери в коротком рассказе 1952 г., посвященном путешествию во времени. До него эту же тему раскрыл Чарльз Гой Форт в двух романах 1923 г., в которых он размышлял о том, что перелет птиц в Нью-Йорке может вызвать ураган в Китае.

(обратно)

Оглавление

Предисловие

Глава 1 Развитие геометрии: Мандельброт против Евклида

Глава 2 Неизвестное измерение. Составление карты Вселенной

Глава 3 О далматинцах и драконах. Линейные фракталы

Глава 4 Скрытый порядок

Библиография

*** Примечания ***